Điểm cuối của góc lượng giác α ở góc phần tư thứ mấy nếu sin 2 α = sin α
A. Thứ III
B. Thứ I hoặc III
C. Thứ I hoặc II
D. Thứ III hoặc IV
Điểm cuối của góc lượng giác α ở góc phần tư thứ mấy nếu cos α = 1 - sin 2 α
A. Thứ II
B. Thứ I hoặc II
C. Thứ II hoặc III
D. Thứ I hoặc IV
Chọn D.
Ta có ![]() tương đương
tương đương ![]()
do đó; cos α = |cos α|
suy ra; cosα ≥ 0
Điểm cuối của góc lượng giác α ở góc phần tư thứ I hoặc IV.
Điểm cuối của α thuộc góc phần tư thứ tư của đường tròn lượng giác. Khẳng định nào sau đây là đúng ?
A. sinα > 0
B. cosα > 0
C. tanα > 0
D. cot α > 0
Chọn B.
Điểm cuối của α thuộc góc phần tư thứ hai nên 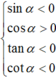
Điểm cuối của α thuộc góc phần tư thứ hai của đường tròn lượng giác. Hãy chọn mệnh đề đúng ?
A. sinα > 0 ; cosα > 0
B. sinα < 0 ; cosα < 0
C. sinα > 0 ; cosα < 0
D. sinα< 0 và cosα > 0
Chọn C.
Điểm cuối của α thuộc góc phần tư thứ hai nên sinα > 0 ; cosα < 0.
Điểm cuối của α thuộc góc phần tư thứ nhất của đường tròn lượng giác. Kết luận nào sau đây là đúng :
A. sinα < 0
B. cosα < 0
C. tanα < 0
D. cotα > 0
Chọn D.
Vì điểm cuối của α thuộc góc phần tư thứ nhất của đường tròn lượng giác nên ta có : sinα > 0; cosα > 0; tanα > 0; cotα > 0
Điểm cuối của α thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai ?
A . sinα > 0
B. cosα < 0
C. tanα > 0
D. cotα > 0
Chọn A.
Điểm cuối của α thuộc góc phần tư thứ hai
Nên 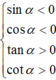
Tính các giá trị lượng giác còn lại của góc α biết sin α = 3 5
A. cos α = 3 4 ; tan α = 3 4 ; c o t α = 4 5
B. cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 3
C. cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 5
B. cos α = 3 4 ; tan α = 4 5 ; c o t α = 4 3
Ta có sin α = 3 5 suy ra sin 2 α = 9 25 , mà sin 2 α + cos 2 α = 1 , do đó:
cos 2 α = 1 - sin 2 α = 1 - 9 25 = 16 25 suy ra cos α = 4 5
Do đó:
tan α = sin α cos α = 3 5 : 4 5 = 3 5 . 5 4 = 3 4
c o t α = cos α sin α = 4 5 : 3 5 = 4 5 . 5 3 = 4 3
Vậy cos α = 4 5 ; tan α = 3 4 ; c o t α = 4 3
Đáp án cần chọn là: B
a) Biết Sin α.cos α=\(\dfrac{12}{25}\). Tính tỉ số lượng giác của góc α
b) Biết Sin α=\(\dfrac{3}{5}\). Tính A=5.Sin2α + 6cos2α
c) Biết cot α=\(\dfrac{4}{3}\). Tính D=\(\dfrac{Sin\alpha+cos\alpha}{Sin\alpha-cos\alpha}\)
b) Ta có: \(\sin^2\alpha+\cos^2\alpha=1\)
\(\Leftrightarrow\cos^2\alpha=\dfrac{16}{25}\)
hay \(\cos\alpha=\dfrac{4}{5}\)
Ta có: \(A=5\cdot\sin^2\alpha+6\cdot\cos^2\alpha\)
\(=5\cdot\left(\dfrac{3}{5}\right)^2+6\cdot\left(\dfrac{4}{5}\right)^2\)
\(=5\cdot\dfrac{9}{25}+6\cdot\dfrac{16}{25}\)
\(=\dfrac{141}{25}\)
c) Ta có: \(\tan\alpha=\dfrac{1}{\cot\alpha}=\dfrac{1}{\dfrac{4}{3}}=\dfrac{3}{4}\)
\(D=\dfrac{\sin\alpha+\cos\alpha}{\sin\alpha-\cos\alpha}\)
\(=\dfrac{\dfrac{9}{16}+\dfrac{16}{9}}{\dfrac{9}{16}-\dfrac{16}{9}}=-\dfrac{337}{175}\)
Điểm cuối của α thuộc góc phần tư thứ nhất của đường tròn lượng giác. Hãy chọn kết quả đúng trong các kết quả sau đây.
A. sinα > 0
B. cosα < 0
C. tanα < 0
D. cotα < 0
Chọn A.
Điểm cuối của α thuộc góc phần tư thứ nhất 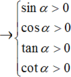
Các bạn trả lời nhanh giúp mình nhé. Mk đang cần gấp lắm.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
1. Tính tỉ số lượng giác của góc nhọn α ( alpha nha )biết:
a) sin α = 0,8
b) tan α = 0,6
c) Câu này hơi khó hơn (sin α + cos α)/ (sin α - cos) α. Nếu các bạn k hiểu thì trả lời cho mình biết nhé
ta co \(sin^2a+cos^2a=1\Rightarrow cosa=0.36\)
\(\frac{sina}{cosa}=tana\Rightarrow tana=\frac{20}{9}\)
\(tana\cdot cotga=1\Rightarrow cotga=\frac{9}{20}\)
câu b tương tự nha cau c \(\frac{sina+cosa}{sina-cosa}=\) bn