Chọn C.
Điểm cuối của α thuộc góc phần tư thứ hai nên sinα > 0 ; cosα < 0.
Chọn C.
Điểm cuối của α thuộc góc phần tư thứ hai nên sinα > 0 ; cosα < 0.
Cho góc α thỏa mãn ![]() và sinα + cosα > 0. Tính P = sin3 α + cos3 α.
và sinα + cosα > 0. Tính P = sin3 α + cos3 α.
![]()
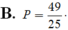
![]()
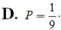
Cho góc α thỏa mãn 0 < α < π 4 và sin α + cos α = 5 2 . Tính P = sinα - cosα
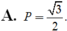 A.
P
=
3
2
A.
P
=
3
2
B. P = 1
C. P = -1/2
D. P = - 3 2
Cho cos α = 4 5 và sin α < 0 , sin β = 3 4 và cos β > 0 . Khi đó sin α + β bằng
A. 3 7 16 - 12 25
B. 4 7 - 9 20
C. - 3 7 + 12 20
D. 12 - 3 7 20
Hãy nêu định nghĩa của sinα , cosα và giải thích vì sao ta có:
sin(α +k2 π)=sinα;k ∈Z
cos(α +k2 π)=cosα;k ∈Z
Xét góc lượng giác (OA; OM) = α, trong đó M là điểm không làm trên các trục tọa độ Ox và Oy. Khi đó M thuộc góc phần tư nào để sinα và cosα cùng dấu
A. I và (II).
B. I và (III).
C. I và (IV).
D. (II) và (III).
Cho góc α thỏa mãn sin α = 12 13 và π 2 < α < π .Tính cosα.
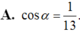
![]()
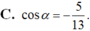
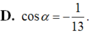
Cho góc α thỏa mãn tanα = 2 và 1800< α< 2700 . Tính P = cosα + sinα
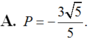
![]()

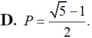
Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với
α = 210 o
Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với
α = 1280 o
Không dùng bảng số và máy tính, hãy xác định dấu của sinα và cosα với
α = 334 o