Chọn A.
Điểm cuối của α thuộc góc phần tư thứ nhất 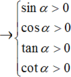
Chọn A.
Điểm cuối của α thuộc góc phần tư thứ nhất 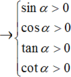
Điểm cuối của α thuộc góc phần tư thứ nhất của đường tròn lượng giác. Kết luận nào sau đây là đúng :
A. sinα < 0
B. cosα < 0
C. tanα < 0
D. cotα > 0
Điểm cuối của α thuộc góc phần tư thứ hai của đường tròn lượng giác. Hãy chọn mệnh đề đúng ?
A. sinα > 0 ; cosα > 0
B. sinα < 0 ; cosα < 0
C. sinα > 0 ; cosα < 0
D. sinα< 0 và cosα > 0
Điểm cuối của α thuộc góc phần tư thứ tư của đường tròn lượng giác. Khẳng định nào sau đây là đúng ?
A. sinα > 0
B. cosα > 0
C. tanα > 0
D. cot α > 0
Điểm cuối của α thuộc góc phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai ?
A . sinα > 0
B. cosα < 0
C. tanα > 0
D. cotα > 0
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O nằm phía trên trục hoành bán kính R = 1 được gọi là nửa đường tròn đơn vị (h.2.2). Nếu cho trước một góc nhọn α thì ta có thể xác định một điểm M duy nhất trên nửa đường tròn đơn vị sao cho ∠(xOM) = α. Giả sử điểm M có tọa độ (xo; yo).
Hãy chứng tỏ rằng sinα = yo, cosα = xo, tanα = yo/xo , cotα = xo/yo .
a) Cho cos α = 2 3 . Tính giá trị của biểu thức
A = tan α + 3 c o t α tan α + c o t α
b) Cho sin α = 3 5 v à 90 ° < α < 180 °
Tính giá trị của biểu thức:
C = c o t α - 2 tan α tan α + 3 c o t α
Biết rằng cung lượng giác α có điểm biểu diễn trên đường tròn lượng giác là M thuộc cung phần tư thứ IV. Mệnh đề nào đúng?
A.sinα>0 B.cosα<0 C.tanα<0 D.cotα>0
NHỚ GIẢI CHI TIẾT NHÉ THANHKSSS~~
Cho a → và b → là hai vectơ cùng hướng và đều khác vectơ 0 → . Trong các kết quả sau đây, hãy chọn kết quả đúng:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Xét góc lượng giác (OA; OM) = α, trong đó M là điểm không làm trên các trục tọa độ Ox và Oy. Khi đó M thuộc góc phần tư nào để sinα và cosα cùng dấu
A. I và (II).
B. I và (III).
C. I và (IV).
D. (II) và (III).