Tứ giác ở hình nào dưới đây là tứ giác nội tiếp
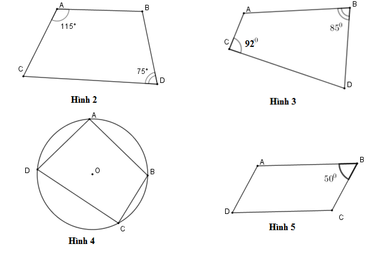
A. Hình 2
B. Hình 3
C. Hình 4
D. Hình 5
Tứ giác ở hình nào dưới đây là tứ giác nội tiếp?
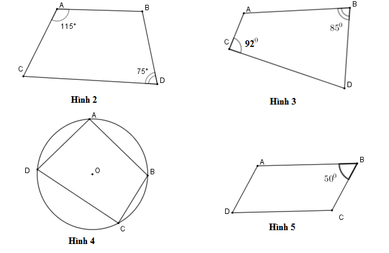
A. Hình 2
B. Hình 3
C. Hình 4
D. Hình 5
Chọn đáp án C
Hình 4 đúng vì tứ giác này có 4 đỉnh cùng thuộc một đường tròn
Hình dưới đây có bao nhiêu hình tam giác, bao nhiêu hình tứ giác ?
A. 4 hình tam giác, 5 hình tứ giác B. 4 hình tam giác, 4 hình tứ giác
C. 5 hình tam giác, 4 hình tứ giác D. 5 hình tam giác, 5 hình tứ giác
Câu 18: Tứ giác nào sau đây nội tiếp được đường tròn ?
A. Hình thang B. Hình thang cân C. Hình thang vuông D. Hình bình hành
Câu 22: Tứ giác nào không nội tiếp được đường tròn?
A. Hình chữ nhật B. Hình thang cân C. Hình thang vuông D. Hình vuông
Trong các tứ giác ở hình dưới đây, hình nào là hình bình hành.
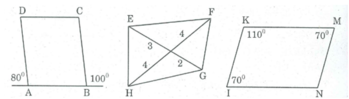
* Tứ giác ABCD là hình bình hành vì AB // CD và AB = CD.
* Tứ giác IKMN có: ∠ I + ∠ K + ∠ N + ∠ M = 360 0
Suy ra: ∠ N = 360 0 - ( ∠ K + ∠ I + ∠ M) = 110 0
Ta có ∠ I = ∠ M = 70 0 và ∠ K = ∠ N = 110 0
Suy ra IKMN là hình bình hành (tứ giác có các góc đối bằng nhau).
* Tứ giác EFGH không là hình bình hành vì có hai đường chéo không cắt nhau tại trung điểm mỗi đường.
Cho hình thang ABCD nội tiếp đường tròn ( O) có đường chéo AC, BD cắt nhau ở E, các cạnh bên AD, BC kéo dài cắt nhau ở F. Chứng minh rằng: a, Tứ giác ABCD là hình thang cân b, FA.FD=FB.FC c, Góc AED = góc AOD d, Tứ giác AOCF nội tiếp
b) Xét ΔFDC có
A\(\in\)FD(gt)
B\(\in\)FC(gt)
AB//CD(gt)
Do đó: \(\dfrac{FA}{AD}=\dfrac{FB}{BC}\)(Định lí Ta lét)
\(\Leftrightarrow\dfrac{FA}{FB}=\dfrac{AD}{BC}=1\)
hay FA=FB
Ta có: FA+AD=FD(A nằm giữa F và D)
FB+BC=FC(B nằm giữa F và C)
mà FA=FB(cmt)
và AD=BC(ABCD là hình thang cân)
nên FD=FC
Ta có: FA=FB(cmt)
FD=FC(cmt)
Do đó: \(FA\cdot FD=FB\cdot FC\)(đpcm)
a) Ta có: ABCD là tứ giác nội tiếp(gt)
nên \(\widehat{A}+\widehat{C}=180^0\)(hai góc đối)(1)
Ta có: ABCD là hình thang(AB//CD)
nên \(\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)(2)
Từ (1) và (2) suy ra \(\widehat{C}=\widehat{D}\)
Hình thang ABCD(AB//CD) có \(\widehat{C}=\widehat{D}\)(cmt)
nên ABCD là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Cho tam giác ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.
a) Tứ giác AEDF là hình gì? Vì sao?
b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?
c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình vuông?
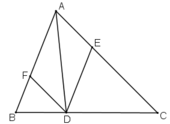
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
Câu 8. _NB_ Để chứng minh tứ giác ABCD là hình vuông, dấu hiệu nào sau đây là sai ? A. Tứ giác ABCD là hình thoi có hai đường chéo bằng nhau. B. Tứ giác ABCD là hình thoi có một góc vuông. C. Tứ giác ABCD là hình thoi có hai đường chéo vuông góc. D. Tứ giác ABCD là hình chữ nhật có hai cạnh kề bằng nhau