Cho hai hàm số f x = 6 x 4 và h ( x ) = 7 − 3. x 2 . So sánh f(−1) và h 2 3
A. f − 1 = h 2 3
B. f − 1 > h 2 3
C. f − 1 < h 2 3
D. Không đủ điều kiện so sánh
Cho hai hàm số y= f(x) và y= g(x) . Hai hàm số y= f’(x) và g’(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y= g’(x).
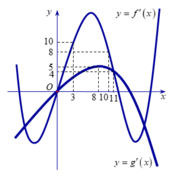
Hàm số h(x)=f(x+4)-g(2x-32) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hai hàm số y=f(x),y=g(x) có đạo hàm là f'(x),g'(x) Đồ thị hàm số f'(x), g'(x) được cho như hinh vẽ dưới đây
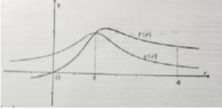
Biết rằng f(0)-f(6)<g(0)-g(6) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [0;6] lần lượt là:
A. h(6),h(2)
B. h(0),h(2)
C. h(2),h(6)
D. h(2),h(0)
Cho hai hàm số F(x)= ( x 2 + a x + b ) e - x v à f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a=1;b= -7
B. a= -1;b= -7
C. a= -1;b=7
D. a=1;b=7
Cho hai hàm số F ( x ) = ( x 2 + a x + b ) e - x và f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a = 1 b = -7
B. a = -1 b = -7
C. a = -1 b = 7
D. a = 1 b = 7
Cho \(f\left( x \right)\) và \(g\left( x \right)\) là hai hàm số có đạo hàm tại \({x_0}\). Xét hàm số \(h\left( x \right) = f\left( x \right) + g\left( x \right)\).
Ta có \(\frac{{h\left( x \right) - h\left( {{x_0}} \right)}}{{x - {x_0}}} = \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} + \frac{{g\left( x \right) - g\left( {{x_0}} \right)}}{{x - {x_0}}}\)
nên \(h'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{h\left( x \right) - h\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} + \mathop {\lim }\limits_{x \to {x_0}} \frac{{g\left( x \right) - g\left( {{x_0}} \right)}}{{x - {x_0}}} = ... + ...\)
Chọn biểu thức thích hợp thay cho chỗ chấm để tìm \(h'\left( {{x_0}} \right)\).
Ta có: \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = f'\left( {{x_0}} \right);\mathop {\lim }\limits_{x \to {x_0}} \frac{{g\left( x \right) - g\left( {{x_0}} \right)}}{{x - {x_0}}} = g'\left( {{x_0}} \right)\)
Vậy \(h'\left( {{x_0}} \right) = f'\left( {{x_0}} \right) + g'\left( {{x_0}} \right)\).
Cho hàm số y=f(x)=2/3.x
a) Tìm f(7); f(-5/4)
b)Tìm x khi y=10
c)Tìm x khi f(x)=8
d)Vẽ đồ thị hàm số trên.
e) Hỏi điểm P(9;16) có thuộc đồ thị hàm số y=2/3 x ko?
g) Tìm điểm K và H trên đồ thị hàm số y=2/3x biết xK =6,yH =4.
Cho hai hàm số f(x) = -2 x 3 và h(x) = 10 - 3x . So sánh f(-2) và h(-1)
A. f(-2) < h(-1)
B. f(-2) ≤ h(-1)
C. f(-2) = h(-1)
D. f(-2) > h(-1)
Đáp án D
Thay x = -2 vào hàm số f(x) = -2 x 3 ta được f(-2) = -2.(-2) = 16 .
Thay x = -1 vào hàm số h(x) = 10 - 3x ta được h(-1) = 10 - 3.(-1) = 13.
Nên f(-2) > h(-1).
Cho hai hàm số f(x) = -2 x 3 và h(x) = 10 - 3x . So sánh f(-2) và h(-1)
A. f(-2) < h(-1)
B. f(-2) ≤ h(-1)
C. f(-2) = h(-1)
D. f(-2) > h(-1)
Đáp án D
Thay x = -2 vào hàm số f(x) = -2 x 3 ta được f(-2) = -2.(-2) = 16 .
Thay x = -1 vào hàm số h(x) = 10 - 3x ta được h(-1) = 10 - 3.(-1) = 13.
Nên f(-2) > h(-1) .
Cho hàm số f(x) có đạo hàm và liên tục trên đoạn [4;8] và f ( x ) ≠ 0 ∀ x ∈ [ 4 ; 8 ] Biết rằng
∫ 4 8 [ f ' ( x ) ] 2 f ( x ) 4 d x = 1 và f(4) = 1/4; f(8) = 1/2; tính F(6)
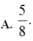
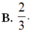
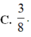
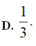
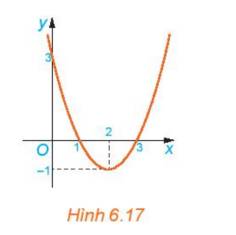
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a