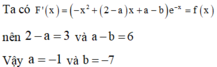Các câu hỏi tương tự
Biết hàm số
F
(
x
)
a
x
3
+
(
a
+
b
)
x
2
+
(
2
a
-
b
+
c
)
x
+
1
là một nguyên hàm của hàm số
f
(
x
)
3
x...
Đọc tiếp
Biết hàm số F ( x ) = a x 3 + ( a + b ) x 2 + ( 2 a - b + c ) x + 1 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 6 x + 2 . Tổng a+b+c là
A. 5.
B. 4.
C. 3.
D. 2.
Biết
F
(
x
)
a
ln
|
x
-
1
|
+
b
ln
|
x
-
2
|
(
a
,
b
∈
Z
)
là một nguyên hàm của hàm số
f
(
x
)
x
+...
Đọc tiếp
Biết F ( x ) = a ln | x - 1 | + b ln | x - 2 | ( a , b ∈ Z ) là một nguyên hàm của hàm số f ( x ) = x + 1 ( x - 1 ) ( x - 2 ) . Giá trị của biểu thức b-a bằng
29 tháng 5 2021 lúc 20:54
xét sự biến thiên của hàm số a)f'(x)=(x+1)⁷(x²-4x)(x-2)³x⁵ b)f'(x)=(x²-7x+6)(-2x+7)/(x-1)³(x-4)² c)f'(x)=(x²-6x+5)(x-1)⁷/x²+3x+2
31 tháng 5 2021 lúc 10:49
xét sự biến thiên của hàm số a)f'(x)=(x+1)⁷(x²-4x)(x-2)³x⁵ b)f'(x)=(x²-7x+6)(-2x+7)/(x-1)³(x-4)² c)f'(x)=(x²-6x+5)(x-1)⁷/x²+3x+2
Giả sử f(x) là hàm số liên tục trên đoạn [a; b], F(x) và G(x) là hai nguyên hàm của f(x). Chứng minh rằng F(b) – F(a) = G(b) – G(a), (tức là hiệu số F(b) – F(a) không phụ thuộc việc chọn nguyên hàm).
Biết luôn có hai số a, b để
F
(
x
)
a
x
+
b
x
+
4
(
4
a
-
b
≠
0
)
là nguyên hàm của hàm số f(x) và thỏa mãn
2
f
2
(
x
)
...
Đọc tiếp
Biết luôn có hai số a, b để F ( x ) = a x + b x + 4 ( 4 a - b ≠ 0 ) là nguyên hàm của hàm số f(x) và thỏa mãn 2 f 2 ( x ) = ( F ( x ) - 1 ) f ' ( x ) . Khẳng định nào dưới đây đúng và đầy đủ nhất?
Cho hàm số y f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y f( x) trên [ a; e]? A.
m
a
x
[
a
,...
Đọc tiếp
Cho hàm số y= f(x) xác định và liên tục trên [ a; e] và có đồ thị hàm số y= f’ (x) như hình vẽ bên. Biết rằng f(a) + f( c)) = f( b) + f( d) . Tìm giá trị lớn nhất và nhỏ nhất của hàm số y= f( x) trên [ a; e]?
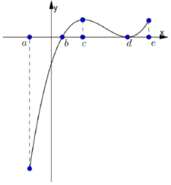
A. m a x [ a , e ] f ( x ) = f ( c ) m i n [ a , e ] f ( x ) = f ( a )
B. m a x [ a , e ] f ( x ) = f ( a ) m i n [ a , e ] f ( x ) = f ( b )
C. m a x [ a , e ] f ( x ) = f ( e ) m i n [ a , e ] f ( x ) = f ( b )
D. m a x [ a , e ] f ( x ) = f ( d ) m i n [ a , e ] f ( x ) = f ( b )
Biết F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] và 2F(a)-12F(b). Tính
I
∫
a
b
f
(
x
)
d
x
. A. I-1. B. I1. C. I
-
1
2
. D. I
1
2
.
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f(x) trên đoạn [a;b] và 2F(a)-1=2F(b). Tính I = ∫ a b f ( x ) d x .
A. I=-1.
B. I=1.
C. I= - 1 2 .
D. I= 1 2 .
Biết F(x) là một nguyên hàm của hàm số
f
(
x
)
10
x
3
-
7
x
+
2
2
x
-
1
thỏa mãn F(1) 5. Giả sử rằng
F
(
3
)
...
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f ( x ) = 10 x 3 - 7 x + 2 2 x - 1 thỏa mãn F(1) = 5. Giả sử rằng F ( 3 ) = a + b 5 , trong đó a,b là các số nguyên. Tính tổng bình phương của a và b
A. 121.
B. 73.
C. 265.
D. 361.