Đường thẳng d đi qua A(1;4) với hệ số góc k có phương trình

y = k(x-1)+4

Phương trình hoành độ giao điểm (P) và d là

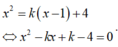
Ta có

Suy ra phương trình trên luôn có hai nghiệm phân biệt và giả sử rằng hai nghiệm đó x₁ < x₂

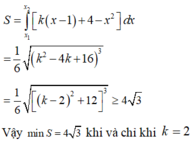
Đáp án B

a: Thay x=1 và y=3 vào (d), ta được:

m+3-m=3

=>3=3(luôn đúng)

b: PTHĐGĐ là:

x^2-mx-3+m=0

=>x^2-mx+m-3=0

Để (d) cắt (P) tại hai điểm phân biệt thì m-3<0

=>m<3

lỗi

a: (d) có hệ số góc là m nên (d): y=mx+b

Thay x=-1 và y=-2 vào (d), ta được:

\(m\cdot\left(-1\right)+b=-2\)

=>b-m=-2

=>b=m-2

=>(d): y=mx+m-2

Phương trình hoành độ giao điểm là:

\(-x^2=mx+m-2\)

=>\(-x^2-mx-m+2=0\)

=>\(x^2+mx+m-2=0\)(1)

\(\text{Δ}=m^2-4\cdot1\cdot\left(m-2\right)\)

\(=m^2-4\left(m-2\right)\)

\(=m^2-4m+8=\left(m-2\right)^2+4>=4\forall m\)

=>(P) luôn cắt (d) tại hai điểm phân biệt

b: Để (P) cắt (d) tại hai điểm nằm về hai phía so với trục tung thì phương trình (1) phải có hai nghiệm phân biệt trái dấu

=>1(m-2)<0

=>m-2<0

=>m<2

Phân tích: Phương trình hoàn độ giao điểm: 

\(x^2+2x-3=x+m\Leftrightarrow x^2+x-3-m=0\left(1\right)\)

\(\left(d\right)\) cắt \(\left(P\right)\) tại 2 điểm phân biệt A ; B 

=> (1) có 2 nghiệm phân biệt 

<=> \(\Delta>0\) \(\Leftrightarrow m>\dfrac{-13}{4}\left(2\right)\)

giả sử: \(A\left(x_1;y_1\right),B\left(x_2;y_2\right)\) với \(x_1;x_2\) là hai nghiệm của (1) Ta phải có :

\(\left(y_1-1\right)\left(y_2-2\right)< 0\Leftrightarrow\left(x_1+m-1\right)\left(x_2+m-1\right)< 0\)

\(\Leftrightarrow x_1x_2+\left(m-1\right)\left(x_1+x_2\right)+m^2-2m+1< 0\)

\(\Leftrightarrow m^2-4m-1< 0\Leftrightarrow2-\sqrt{5}< m< 2+\sqrt{5}\left(thỏa\left(2\right)\right)\)

\(m\in Z\Rightarrow m\in\left\{0;1;2;3;4\right\}\)

a) Khi \(m=1\) \(\Rightarrow\left(d\right):y=2x+8\)

Xét phương trình hoành độ giao điểm

  \(x^2=2x+8\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)

+) Với \(x=4\Rightarrow y=16\)

+) Với \(x=-2\Rightarrow y=4\)

  Vậy khi \(m=1\) thì (P) cắt (d) tại 2 điểm phân biệt \(\left(4;16\right)\) và \(\left(-2;4\right)\)

b) Xét phương trình hoành độ giao điểm

  \(x^2-2x+m^2-9=0\)  (*)

Ta có: \(\Delta'=10-m^2\) 

Để (P) cắt (d) \(\Leftrightarrow\) Phương trình (*) có 2 nghiệm phân biệt 

\(\Leftrightarrow\Delta'=10-m^2>0\) \(\Leftrightarrow-\sqrt{10}< m< \sqrt{10}\)

Theo đề: (P) cắt (d) tại 2 điểm nằm về 2 phía của trục tung

\(\Leftrightarrow\) Phương trình (*) có 2 nghiệm trái dấu

\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\x_1x_2< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}10-m^2>0\\m^2-9< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{10}< m< \sqrt{10}\\-3< m< 3\end{matrix}\right.\) \(\Leftrightarrow-3< m< 3\)

  Vậy ...