Hàm số y = a x 4 + b x + c a ≠ 0 có 1 cực tiểu và 2 cực đại khi và chỉ khi
A. a > 0 b > 0
B. a < 0 b ≥ 0
C. a < 0 b > 0
D. a > 0 b ≠ 0
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho điểm A(3; 4) và hàm số y = 4/3 x .
a) Điểm A có thuộc đồ thị của hàm số y = 4/3 x hay không? Vì sao?
b) Vẽ đồ thị của hàm số y = 4/3 x .
c) Xác định các điểm H(3; 0), P(6; 0), Q(0; 4) trên mặt phẳng tọa độ Oxy ở trên.
d) Chứng minh AO = AP
a: \(y=\dfrac{4}{3}\cdot3=4\)
=>A có thuộc đồ thị
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm A(3; 4) và hàm số y = 4/3 x .
a) Điểm A có thuộc đồ thị của hàm số y = 4/3 x hay không? Vì sao?
b) Vẽ đồ thị của hàm số y = 4/3 x .
c) Xác định các điểm H(3; 0), P(6; 0), Q(0; 4) trên mặt phẳng tọa độ Oxy ở trên.
d) Tam giác AOP là tam giác gì? Vì sao? Tính diện tích của tam giác AOP.
a: y=4/3x3=4
=>A có thuộc đồ thị y=4/3x
Đúng 0
Bình luận (0)
cho hàm số y=f(x) có f'(x)=-3(x+4)(x^2-4)(x+1)^2-2x+12 hỏi hàm số f(x) nghịch biến trong khoảng nào sau đây? A. (−∞; -1) B. (0; 2) C. (2; +∞) D. (-1; 0)
Tìm khẳng định sai trong các khẳng định sau đây:A. Hàm số y 4cosx - 5
sin
2
x
- 3 là hàm số chẵn;B. Đồ thị hàm số sau có hai tiệm cận đứng
y
3
x
2
-
2
x
+...
Đọc tiếp
Tìm khẳng định sai trong các khẳng định sau đây:
A. Hàm số y = 4cosx - 5 sin 2 x - 3 là hàm số chẵn;
B. Đồ thị hàm số sau có hai tiệm cận đứng y = 3 x 2 - 2 x + 5 x 2 + x - 7
C. Hàm số y = 3 x - 2 3 x + 4 luôn nghịch biến;
D. Hàm số f x = - 2 x với x ≥ 0 sin x 3 với x < 0
không có đạo hàm tại x = 0.
Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì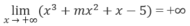 
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.
Đúng 0
Bình luận (0)
5 tháng 8 2023 lúc 9:58
Câu 25. Cho hàm số \(y = \dfrac{x + 1}{x - 1}, y = -x^3+x^2-3x+1, y = x^4 + 2x^2 +2.\) Trong các hàm số trên, có bao nhiêu hàm số đơn điệu trên \(R\)?
A. 1. B. 3. C. 0. D. 2.
\(y'_1=-\dfrac{2}{\left(x-1\right)^2}\) nghịch biến trên R/{1}
\(y'_2=-3x^2+2x-3\) có nghiệm khi y' = 0
\(y'_3=4x^3+4x\) có nghiệm khi y' = 0
Vậy không có hàm số đơn điệu trên R.
Đúng 2
Bình luận (1)
Cho hàm số
y
f
(
x
)
có đạo hàm trên khoảng
a
;
b
. Xét các mệnh đề sau: I. Nếu hàm số
y
f
(
x
)
đồng biến trên khoảng
a
;
b
thì
f...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng
Đúng 0
Bình luận (0)
Câu4 :Cho hàm số y f(x) 2x. Khẳng định nào sau đây đúng?
A. f(0) 0
B. f(1) 6
C. f(-1) 10
D. f(2) -4
Câu 5:Một hàm số được cho bẳng công thức y f(x) x2 ( x bình phương) Khẳng định nào sau đây đúng?
A. f(1) 6
Câu6:Cho hàm số y f(x) 2 + 8x. Khẳng định nào sau đây đúng?
A. f(0) 0
B. f(1) 10
C. f(-1) 10
D. f(2) -4
Câu7:Một hàm số được cho bẳng công thức y f(x) 2x. Tính f(-5) + f(5). KẾT QUẢ ĐÚNG LÀ
A. 0
B. 25
C. 50
D. 10
Đọc tiếp
Câu4 :Cho hàm số y = f(x) = 2x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 6 C. f(-1) = 10 D. f(2) = -4 Câu 5:Một hàm số được cho bẳng công thức y = f(x) = x2 ( x bình phương) Khẳng định nào sau đây đúng? A. f(1) = 6 Câu6:Cho hàm số y = f(x) = 2 + 8x. Khẳng định nào sau đây đúng? A. f(0) = 0 B. f(1) = 10 C. f(-1) = 10 D. f(2) = -4 Câu7:Một hàm số được cho bẳng công thức y = f(x) = 2x. Tính f(-5) + f(5). KẾT QUẢ ĐÚNG LÀ A. 0 B. 25 C. 50 D. 10
hàm số: y=f(x)=ax^2+bx+c
a) xác định các hệ số a;b;c biết: f(0)=5; f(1)=0; f(5)=0
b) trong 2 điểm P(-1;3) và Q(1/2; 9/4) điểm nào thuộc đồ thị hàm số
c) tìm x biết: y=5
Cho hàm số
y
f
x
xác định, liên tục và có đạo hàm trên đoạn
a
,
b
.
Xét các khẳng định sau: 1. Hàm số
f
x
đồng biến trên
a
;
b
thì
f
x
0
,
∀
x
∈...
Đọc tiếp
Cho hàm số y = f x xác định, liên tục và có đạo hàm trên đoạn a , b . Xét các khẳng định sau:
1. Hàm số f x đồng biến trên a ; b thì f ' x > 0 , ∀ x ∈ a ; b
2. Giả sử f a > f c > f b , ∀ x ∈ a ; b suy ra hàm số nghịch biến trên a ; b
3. Giả sử phương trình f ' x = 0 có nghiệm là x = m khi đó nếu hàm số y = f x đồng biến trên m ; b thì hàm số y = f x nghịch biến trên a , m
4. Nếu f ' x ≥ 0 , ∀ x ∈ a ; b , thì hàm số đồng biến trên a ; b
Số khẳng định đúng trong các khẳng định trên là
A. 1
B. 0
C. 3
D. 2
Đáp án A
Phương pháp:
Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.
Cách giải:
*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và f c 2
*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số y = x 3
*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.
Chú ý khi giải:
HS thường nhầm lẫn:
- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.
- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.
Đúng 0
Bình luận (0)
Bài 1 : Cho hàm số y = f(x)=\(\frac{a}{2}.x+b\)
a. Tìm a và b biết các điểm sau thuộc đồ thị hàm số : A( -4; -3 ) ; B(0; -3)
b. Tính f(1), f(2) , f(-2), f(-1)
c. Tìm x biết y bằng 4
a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{2}a\cdot\left(-4\right)+b=-3\\\dfrac{1}{2}a\cdot0+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2a+b=-3\\b=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-3\\a=0\end{matrix}\right.\)
Vậy: f(x)=-3
b: f(1)=f(2)=f(-2)=f(-1)=-3
c: Đặt y=4
=>f(x)=4
=>-3=4(vô lý)
Đúng 0
Bình luận (0)