Ta có 

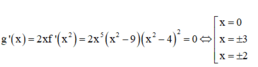
Bảng biến thiên của hàm số y= g( x)

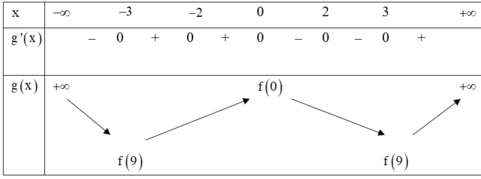
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞)  hàm số nghịch biến trong khoảng (-∞; -3) .

Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3

Vậy có 3 khẳng định đúng là khẳng định I, II, IV

Chọn C.

a)\(f\left(1\right)=2.1^2+5.1-3=2+5-3=4\)

\(f\left(0\right)=0+0-3=-3\)

\(f\left(1,5\right)=2.\left(1,5\right)^2-5.1,5-3=4,5-7,5-3=-6\)

b)\(f\left(3\right)=3a-3=9=>>3a=12=>a=4\)

\(f\left(5\right)=5a-3=11=>5a=14=>a=\dfrac{14}{5}\)

\(f\left(-1\right)=-a-3=6=>-a=9=>a=-9\)

Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.

bài này không khó nghe em chẳng qua là nó hơi dài

em phải nhớ công thức tính tổng của dãy số, công thức tổng quát ấy là n.(a1+an)/2 (n là số số hạng, a1 là phần tử thứ nhất và an là phần tử thứ n)

số số hạng thì dễ rồi đúng k

còn a1+an là bằng f(1/2019)+f(2018/2019)

em thế f(1/2019) vào f(x) cái kia cũng vậy

xong em chịu khó nhân vào có dạng là a^n.a^m

vậy là ra thôi em

Ý bạn là \(f(x)=\frac{1}{9+x^2}+\frac{3}{9+x^2}\) hay thế nào? Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo để được hỗ trợ tốt hơn).

a: \(f\left(x\right)=\sqrt{x^2-6x+9}=\sqrt{\left(x-3\right)^2}=\left|x-3\right|\)

\(f\left(-1\right)=\left|-1-3\right|=4\)

\(f\left(5\right)=\left|5-3\right|=\left|2\right|=2\)

b: f(x)=10

=>\(\left[{}\begin{matrix}x-3=10\\x-3=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=13\\x=-7\end{matrix}\right.\)

c: \(A=\dfrac{f\left(x\right)}{x^2-9}=\dfrac{\left|x-3\right|}{\left(x-3\right)\left(x+3\right)}\)

TH1: x<3 và x<>-3

=>\(A=\dfrac{-\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{-1}{x+3}\)

TH2: x>3

\(A=\dfrac{\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{1}{x+3}\)