Vi phân của hàm số f ( x ) = 3 x 2 – x tại điểm x= 2, ứng với ∆x= 0,1 là:
A. - 4
B. 11
C. 1,1
D. -0,4
Vi phân của hàm số f(x) = 3x2 - x tại điểm x = 2, ứng với Δx = 0,1 là:
A. -0,07.
B. 10.
C. 1,1.
D. -0,4.
Chọn D.
Ta có: f’(x) = 6x – 1 ⇒ f’(2) = 11
df(2) = f’(2) Δx = 11.0,1 = 1,1
Vi phân của hàm số f(x) = sin(3x – 2) + cos(x2 + 1) tại điểm x = 0 ứng với Δx = 0,5 xấp xỉ bằng:
A: -0,24
B: -0,624
C: -0,364
D: Đáp án khác
Chọn B.
Ta có:
f’(x) = 3cos(3x – 2) – 2x.sin(x2 + 1)
Nên df(xo) = f’(xo). Δx = [3cos(3.0 – 2) – 2.0.sin(0 + 1)].0,5 ≈ -0,624
Tìm vi phân của hàm số f(x) = tan2x – sin2(x + 1) tại điểm x = -1 ứng với Δx = -0,02 xấp xỉ bằng:
A: -0.233
B: -0,212
C: -0.312
D: -,0231
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
cho hàm số y=f(x)=(x+4)|x+2| tìm m để hàm số y=f(x) cắt đường thẳng y=m tại 3 điểm phân biệt
Cho hàm số f(x) có đạo hàm cấp hai f''(x) liên tục trên R và đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x=1 đường thẳng △ trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x=2 Tích phân ∫ 0 ln 3 e x f ' ' e x + 1 2 d x bằng
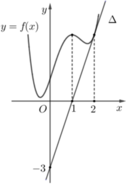
A. 8
B. 4
C. 3
D. 6
Cho hàm số f(x) có đạo hàm cấp hai f''(x) liên tục trên R và có đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x = 1 đường thẳng ![]() trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 . Tích phân
∫
0
ln
3
e
x
f
"
e
x
+
1
2
d
x
bằng
trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 . Tích phân
∫
0
ln
3
e
x
f
"
e
x
+
1
2
d
x
bằng
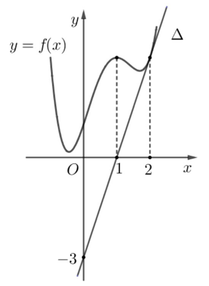
A. 8
B. 4
C. 3
D. 6
Cho hàm số f(x) có đạo hàm cấp hai f'''(x) liên tục trên R và đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x=1; đường thẳng ∆ trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x=2. Tích phân ∫ 0 ln 3 e x f ' ' ( e x + 1 2 ) d x bằng
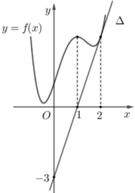
A. 8
B. 4
C. 3
D. 6
Chọn đáp án D
![]()
![]()
![]()
![]()
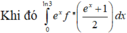
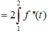

![]()
Do hàm số đạt cực đại tại điểm x=1⇒ f′(1) = 0 và đường thẳng Δ qua hai điểm (0;−3);(1;0) nên có phương trình y=3x−3.
Vì Δ là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 ⇒ f ' ( 2 ) = k △ =3
Vậy
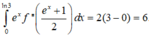
Xét ba mệnh đề sau:
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó.
(2) Nếu hàm số f(x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Trong ba câu trên:
A. Có hai câu đúng và một câu sai.
B. Có một câu đúng và hai câu sai.
C. Cả ba đều đúng.
D. Cả ba đều sai.
Đáp án A
(1) Nếu hàm số f(x) có đạo hàm tại điểm x = x 0 thì f(x) liên tục tại điểm đó. Đây là mệnh đề đúng.
(2) Nếu hàm số f (x) liên tục tại điểm x = x 0 thì f(x) có đạo hàm tại điểm đó.
Phản ví dụ
Lấy hàm f ( x ) = x ta có D= R nên hàm số f(x) liên tục trên R.
Nhưng ta có l i m x → 0 + f ( x ) - f ( 0 ) x - 0 = l i m x → 0 + x - 0 x - 0 = l i m x → 0 + x - 0 x - 0 = 1 l i m x → 0 - f ( x ) - f ( 0 ) x - 0 = l i m x → 0 - x - 0 x - 0 = l i m x → 0 - - x - 0 x - 0 = - 1
Nên hàm số không có đạo hàm tại x = 0.
Vậy mệnh đề (2) là mệnh đề sai.
(3) Nếu f(x) gián đoạn tại x = x 0 thì chắc chắn f(x) không có đạo hàm tại điểm đó.
Vì (1) là mệnh đề đúng nên ta có f(x) không liên tục tại x = x 0 thì f(x) không có đạo hàm tại điểm đó.
Vậy (3) là mệnh đề đúng.