Chọn B.
Ta có:
f’(x) = 3cos(3x – 2) – 2x.sin(x2 + 1)
Nên df(xo) = f’(xo). Δx = [3cos(3.0 – 2) – 2.0.sin(0 + 1)].0,5 ≈ -0,624
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Tìm vi phân của hàm số f(x) = tan2x – sin2(x + 1) tại điểm x = -1 ứng với Δx = -0,02 xấp xỉ bằng:
A: -0.233
B: -0,212
C: -0.312
D: -,0231
Vi phân của hàm số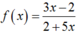 
tại điểm x = -1 ứng với Δx = 0,01 xấp xỉ bằng
A: 0,18
B: 0,018
C: 0,17
D: 0,017
Tìm vi phân của hàm số 
tại điểm x = 1 ứng với Δx = 0,5.
A: 1
B: -1
C: 0
D: 2
Vi phân của hàm số f(x) = 3x2 - x tại điểm x = 2, ứng với Δx = 0,1 là:
A. -0,07.
B. 10.
C. 1,1.
D. -0,4.
Cho hàm số
f
(
x
x
3
+
b
x
2
+
c
x
+
d
,
C
g
x
x
2
-
3
x
+
1
Với các số b, c, d tìm được ở bài 19, hãy:a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ...
Đọc tiếp
Cho hàm số f ( x = x 3 + b x 2 + c x + d , C g x = x 2 - 3 x + 1
Với các số b, c, d tìm được ở bài 19, hãy:
a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = - 1 .
b) Giải phương trình f ' sin x = 0 .
c) tính lim x → 0 f ' ' sin 5 x + 1 g ' sin 3 x + 3
Số gia của hàm số
f
(
x
)
x
2
ứng với số gia δx của đối số x tại
x
0
-
1
là A.
∆
x
2
-
2
∆
x
-
1
B.
∆
x
2
+
2...
Đọc tiếp
Số gia của hàm số f ( x ) = x 2 ứng với số gia δx của đối số x tại x 0 = - 1 là
A. ∆ x 2 - 2 ∆ x - 1
B. ∆ x 2 + 2 ∆ x + 2
C. ∆ x 2 + 2 ∆ x
D. ∆ x 2 - 2 ∆ x
Cho hàm số
f
(
x
)
x
2
-
x
, đạo hàm của hàm số ứng với số gia Δx của đối số x tại
x
0
là A.
lim
∆
x
→
0
∆
x
2
+
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - x , đạo hàm của hàm số ứng với số gia Δx của đối số x tại x 0 là
A. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x - ∆ x
B. lim ∆ x → 0 ∆ x + 2 x - 1
C. lim ∆ x → 0 ∆ x + 2 x + 1
D. lim ∆ x → 0 ∆ x 2 + 2 x ∆ x + ∆ x
Cho hàm số
f
(
x
)
x
2
-
x
, đạo hàm của hàm số ứng với số gia Δx của đối số x tại
x
0
là: A.
lim
∆
x
→
0
∆
x
2
-
2...
Đọc tiếp
Cho hàm số f ( x ) = x 2 - x , đạo hàm của hàm số ứng với số gia Δx của đối số x tại x 0 là:
A. lim ∆ x → 0 ∆ x 2 - 2 x 0 ∆ x - ∆ x
B. lim ∆ x → 0 ∆ x + 2 x 0 - 1
C. lim ∆ x → 0 ∆ x + 2 x 0 + 1
D. lim ∆ x → 0 ∆ x 2 + 2 x 0 ∆ x + ∆ x
Số gia của hàm số
f
(
x
)
x
2
2
ứng với số gia Δx của biến số x tại
x
0
-
1
là A.
1
2
∆
x
2
-
∆
x
B.
1
2...
Đọc tiếp
Số gia của hàm số f ( x ) = x 2 2 ứng với số gia Δx của biến số x tại x 0 = - 1 là
A. 1 2 ∆ x 2 - ∆ x
B. 1 2 ∆ x 2 - ∆ x
C. 1 2 ∆ x 2 + ∆ x
D. 1 2 ∆ x 2 + ∆ x