a) \(\sin \left( {x + h} \right) - \sin x = 2\cos \frac{{2x + h}}{2}.\sin \frac{h}{2}\)

b) Với \({x_0}\) bất kì, ta có:

\(\begin{array}{l}f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin x - \sin {x_0}}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{2\cos \frac{{x + {x_0}}}{2}.\sin \frac{{x - {x_0}}}{2}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin \frac{{x - {x_0}}}{2}}}{{\frac{{x - {x_0}}}{2}}}.\mathop {\lim }\limits_{x \to {x_0}} \cos \frac{{x + {x_0}}}{2} = \cos {x_0}\end{array}\)

Vậy hàm số y = sin x  có đạo hàm là hàm số \(y' = \cos x\)

Lời giải:
$f'(x)=5(\sin ^23x-4)'(\sin ^23x-4)^4=5.2.\sin 3x (\sin 3x)'.(\sin ^23x-4)^4$

$=30\sin 3x\cos 3x(\sin ^23x-4)^4$

$\Rightarrow k=30$

a) Hàm số \(f\left( x \right) = {x^2} + \sin x\) có tập xác định là \(\mathbb{R}\).

Hàm số x² và sinx liên tục trên \(\mathbb{R}\) nên hàm số \(f\left( x \right) = {x^2} + \sin x\) liên tục trên \(\mathbb{R}\).

b) Hàm số \(g\left( x \right) = {x^4} - {x^2} + \frac{6}{{x - 1}}\) có tập xác định là \(\mathbb{R}\backslash \left\{ 1 \right\}.\)

Hàm số \({x^4} - {x^2}\) liên tục trên toàn bộ tập xác định

Hàm số \(\frac{6}{{x - 1}}\) liên tục trên các khoảng \(\left( {-\infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)

Vậy hàm số đã cho liên tục trên các khoảng \(\left( {-\infty ;1} \right)\) và \(\left( {1; + \infty } \right).\)

c) Hàm số \(h\left( x \right) = \frac{{2x}}{{x - 3}} + \frac{{x - 1}}{{x + 4}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ {-4;3} \right\}.\)

Hàm số \(\frac{{2x}}{{x - 3}}\)  liên tục trên các khoảng \(\left( {-\infty ;3} \right)\) và \(\left( {3; + \infty } \right).\)

Hàm \(\frac{{x - 1}}{{x + 4}}\)  liên tục trên các khoảng \(\left( {-\infty ;-4} \right)\) và \(\left( {-4; + \infty } \right).\)

Vậy hàm số đã cho liên tục trên các khoảng  \(\left( {-\infty ;-4} \right)\), \(\left( {-4;3} \right)\), \(\left( {3; + \infty } \right).\)

Với bất kì \({x_0} \in \mathbb{R}\), ta có:

\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin x - \sin {x_0}}}{{x - {x_0}}}\)

Đặt \(x = {x_0} + \Delta x\). Ta có:

\(\begin{array}{l}f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin \left( {{x_0} + \Delta x} \right) - \sin {x_0}}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\cos \Delta x + \cos {x_0}\sin \Delta x - \sin {x_0}}}{{\Delta x}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\cos \Delta x - \sin {x_0}}}{{\Delta x}} + \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\cos {x_0}\sin \Delta x}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( {\cos \Delta x - 1} \right)}}{{\Delta x}} + \mathop {\lim }\limits_{\Delta x \to 0} \cos {x_0}.\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin \Delta x}}{{\Delta x}}\end{array}\)

Lại có:

\(\begin{array}{l}\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( {\cos \Delta x - 1} \right)}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( {\cos \Delta x - 1} \right)\left( {\cos \Delta x + 1} \right)}}{{\Delta x\left( {\cos \Delta x + 1} \right)}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( {{{\cos }^2}\Delta x - 1} \right)}}{{\Delta x\left( {\cos \Delta x + 1} \right)}}\\ = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}\left( { - {{\sin }^2}\Delta x} \right)}}{{\Delta x\left( {\cos \Delta x + 1} \right)}} =  - \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin \Delta x}}{{\Delta x}}.\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin {x_0}.\sin \Delta x}}{{\left( {\cos \Delta x + 1} \right)}} =  - 1.\frac{{\sin {x_0}.\sin 0}}{{\cos 0 + 1}} = 0\\\mathop {\lim }\limits_{\Delta x \to 0} \cos {x_0}.\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\sin \Delta x}}{{\Delta x}} = \cos {x_0}.1 = \cos {x_0}\end{array}\)

Vậy \(f'\left( {{x_0}} \right) = \cos {x_0}\)

Vậy \(f'\left( x \right) = \cos x\) trên \(\mathbb{R}\).

Biến đổi :

\(4\sin^2x+1=5\sin^2x+\cos^2x=\left(a\sin x+b\cos x\right)\left(\sqrt{3}\sin x+\cos x\right)+c\left(\sin^2x+\cos^2x\right)\)

\(=\left(a\sqrt{3}+c\right)\sin^2x+\left(a+b\sqrt{3}\right)\sin x.\cos x+\left(b+c\right)\cos^2x\)

Đồng nhấtheej số hai tử số 

\(\begin{cases}a\sqrt{3}+c=5\\a+b\sqrt{3}=0\\b+c=1\end{cases}\)

\(\Leftrightarrow\) \(\begin{cases}a=\sqrt{3}\\b=-1\\c=2\end{cases}\)

Đặt \(sinx=t\Rightarrow t\in\left[-\dfrac{1}{2};1\right]\)

\(y=f\left(t\right)=2t^2+t+4\)

Xét hàm \(f\left(t\right)=2t^2+t+4\) trên \(\left[-\dfrac{1}{2};1\right]\)

\(-\dfrac{b}{2a}=-\dfrac{1}{4}\in\left[-\dfrac{1}{2};1\right]\)

\(f\left(-\dfrac{1}{2}\right)=4\) ; \(f\left(-\dfrac{1}{4}\right)=\dfrac{31}{8}\); \(f\left(1\right)=7\)

\(y_{max}=7\) khi \(t=1\) hay \(x=\dfrac{\pi}{2}\)

\(y_{min}=\dfrac{31}{8}\) khi \(sinx=-\dfrac{1}{4}\)

Biến đổi :

\(4\sin x+3\cos x=A\left(\sin x+2\cos x\right)+B\left(\cos x-2\sin x\right)=\left(A-2B\right)\sin x+\left(2A+B\right)\cos x\)

Đồng nhất hệ số hai tử số, ta có :

\(\begin{cases}A-2B=4\\2A+B=3\end{cases}\)\(\Leftrightarrow\begin{cases}A=2\\B=-1\end{cases}\)

Khi đó \(f\left(x\right)=\frac{2\left(\left(\sin x+2\cos x\right)\right)-\left(\left(\sin x-2\cos x\right)\right)}{\left(\sin x+2\cos x\right)}=2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\)

Do đó, 

\(F\left(x\right)=\int f\left(x\right)dx=\int\left(2-\frac{\cos x-2\sin x}{\sin x+2\cos x}\right)dx=2\int dx-\int\frac{\left(\cos x-2\sin x\right)dx}{\sin x+2\cos x}=2x-\ln\left|\sin x+2\cos x\right|+C\)

+ Xét hàm số  y= f(x) = cos3x

TXĐ: D =R

Với mọi x ∈ D , ta có: - x ∈ D  và

   f( -x) = cos( - 3x) = cos3x = f(x)

Do đó, y= cos 3x là hàm chẵn trên tập xác định của nó.

+ Xét hàm y= g(x)= sin(x² + 1)

TXĐ: D= R

Với mọi x ∈ D , ta có: - x ∈ D  và

 g( -x)= sin[ (-x)² +1]= sin( x²+1)= g(x)

    Do đó: y= sin( x² +1)  là hàm chẵn trên R.

    + Xét hàm số y= h( x)= tan²x .

    TXĐ: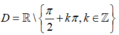 

Với mọi x ∈ D , ta có: - x ∈ D  và

    h( -x)= tan² (-x)= (- tanx)² = tan² x=  h(x)

Do đó y= tan²x là hàm số chẵn trên D.

+ Xét hàm số y= t(x)= cotx.

    TXĐ:  

Với mọi x ∈ D , ta có: - x ∈ D  và t(-x)= cot(-x) = - cotx = - t(x)

Do đó:  y= cotx là hàm số lẻ trên D.

Vậy (1); (2); (3) là các hàm số chẵn

Đáp án C

a) Tập xác định của hàm số là \(D = \mathbb{R}\)

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D

Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) =  - \sin x =  - f\left( x \right),\;\forall x\; \in \;D\)

Vậy \(y = \sin x\) là hàm số lẻ.

b)

c) Từ đồ thị trên, ta thấy hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right),\;k\; \in \;\mathbb{Z}.\)

Đáp án A

Hàm số chẵn là: y = cos x