Cho tam giác OAB . Gọi N là trung điểm của OB . Các số m ; n thỏa mãn đẳng thức A N → = m O A → + n O B → . Khẳng định nào sau đây đúng?
A.m= -1; n= ½
B. m= -4; n= 1
C. m= -2; n=1.
D.m= 1; n= -1/2.
Cho tam giác OAB. Gọi M, N lần lượt là trung điểm của OA và OB. Tìm các số m, n sao cho:
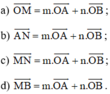
Cho tam giác OAB . Gọi N là trung điểm của OB . Các số m ; n thỏa mãn đẳng thức A N → = m O A → + n O B → Khẳng định nào sau đây đúng?
A. m = -1; n = ½.
B. m = -4; n = 1.
C. m = -2; n = 1.
D. m = 1; n = -1/2.
Cho tam giác OAB vuông tại O. Gọi M,N lần lượt là trung điểm các chạnh OA và OB. Biết OA= 21 cm, OB = 28 cm
a/ Tính MN
b/ Tính diện tích tam giác OMN.
a, Canh ON la : 28/2=14 cm
Canh OM la : 21/2=10,5
Áp dụng định lý pi-ta-go :
ON2+OM2=MN2
142+10,52=MN2
=>MN=17,5
b , Diện tích tam giác OMN là :
1/2.14.10,5=73,5(cm2)
k mk nha
Cho tam giác OAB. Gọi M và N lần lượt là trung điểm của OA và OB. Tìm các số m, n sao cho :
a) \(\overrightarrow{OM}=m\overrightarrow{OA}+n\overrightarrow{OB}\)
b) \(\overrightarrow{AN}=m\overrightarrow{OA}+n\overrightarrow{OB}\)
c) \(\overrightarrow{MN}=m\overrightarrow{OA}+n\overrightarrow{OB}\)
d) \(\overrightarrow{MB}=m\overrightarrow{OA}+n\overrightarrow{OB}\)
b)
\(\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AO}=-\dfrac{1}{2}\overrightarrow{OA}\)
Vậy \(m=-\dfrac{1}{2};n=0\).
c)
\(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AB}=\dfrac{1}{2}\left(\overrightarrow{AO}+\overrightarrow{OB}\right)=-\dfrac{1}{2}\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{OB}\).
Vậy \(m=-\dfrac{1}{2};n=\dfrac{1}{2}\).
d)
\(\overrightarrow{MB}=\dfrac{1}{2}\overrightarrow{OB}\)
Vậy \(m=0;n=\dfrac{1}{2}\).
Cho tam giác OAB, điểm C thuộc OB sao cho OC=1/2CB. Gọi D là trung điểm của AB. E là giao điểm của OD và AC. Chứng Minh OE=ED
cho tam giác abc và o là một điểm thuộc miền trong của tam giác gọi d,e,f lần lượt là trung ddiemr của các cạnh ab,bc,ca và l,m,n lần lượt là trung điểm của các đoạn oa, ob,oc
Cho tam giác ABC và một điểm O nằm trong tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Trên tia OM, ON, OP lấy các điểm A’, B’, C’ sao cho M, N, P theo thứ tự là trung điểm của các đoạn thẳng OA’, OB’, OC’. Chứng mình rằng tam giác ABC bằng tam giác A’B’C’.
Cho góc nhọn xoy . Trên tia ox lấy điểm A , trên tia Oy lấy điểm B sao cho OA =OB . Gọi M là trung điểm của
. 1) Chứng minh tam giác oma =omb .
2) Trên tia om lấy k sao cho m nằm giữa o và k . Chứng minh ak =bk
3) Giả sừ xoy =180 độ . Tính số đo oab ?
4) Qua k kẻ đường thẳng song song với ab cắt ox tại e và oy tại f . Gọi n là giao điểm của af và be. Chứng minh rẳng o,m,n thẳng hàng
1: Xét ΔOMA và ΔOMB có
OM chung
MA=MB
OA=OB
Do đó: ΔOMA=ΔOMB
Cho tam giác OAB đều cạnh a. Trên đường thẳng d qua O và vuông góc với mặt phẳng (OAB) lấy điểm M sao cho OM=x. Gọi E, F lần lượt là hình chiếu vuông góc của A trên MB và OB. Gọi N là giao điểm của EF và OM. Tìm x để thể tích tứ diện ABMN có giá trị nhỏ nhất
A. x = a 2 .
B. x = a 2 2 .
C. x = a 6 12 .
D. x = a 3 2 .
Đáp án B

Ta có
A F ⊥ O B , A F ⊥ M O ⇒ A F ⊥ M O B ⇒ A F ⊥ M B
Mà M B ⊥ A E nên M B ⊥ A E F ⇒ M B ⊥ E F .
Suy ra Δ M O B ∽ Δ M E N , mà Δ M E N ∽ Δ F O N nên Δ M O B ∽ Δ F O N . Khi đó O B O M = O N O F ⇒ O N = O B . O F O M = a . a 2 x = a 2 2 x .
Từ
V A B M N = V M . O A B + V N . O A B = 1 3 . S Δ O A B . O M + O N = 1 3 . a 2 3 4 . x + a 2 2 x
⇒ V A B M N = a 2 3 12 x + a 2 2 x ≥ a 2 3 12 .2 x . a 2 2 x = a 2 3 12 . 2 a = a 3 6 12
Dấu “=” xảy ra
⇔ x = a 2 2 x ⇔ 2 x 2 = a 2 ⇔ x = a 2 2 .