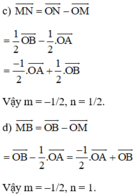Các câu hỏi tương tự
Cho tam giác OAB . Gọi N là trung điểm của OB . Các số m ; n thỏa mãn đẳng thức
A
N
→
m
O
A
→
+
n
O
B
→
Khẳng định nào sau đây đúng? A. m -1; n ½. B. m -4; n 1. C. m -2; n 1. D. m 1; n -1/2.
Đọc tiếp
Cho tam giác OAB . Gọi N là trung điểm của OB . Các số m ; n thỏa mãn đẳng thức A N → = m O A → + n O B → Khẳng định nào sau đây đúng?
A. m = -1; n = ½.
B. m = -4; n = 1.
C. m = -2; n = 1.
D. m = 1; n = -1/2.
Cho hình bình hành ABCD tâm O. Xác định vị trí điểm M thỏa mãn \(\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{AM}\). Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và dựng điểm K sao cho \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\). Khi đó, điểm K trùng với
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).a/ Tìm tọa độ trọng tâm G của tam giác ABC.b/ Tìm tọa độ điểm D để ABCD là hình bình hànhc/ Tìm tọa độ sao cho Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng:
Đọc tiếp
Câu 1: Cho tam giác ABC có A(3,2); B(4,1) và C(1,5).
a/ Tìm tọa độ trọng tâm G của tam giác ABC.
b/ Tìm tọa độ điểm D để ABCD là hình bình hành
c/ Tìm tọa độ ![]() sao cho
sao cho ![]()
Câu 2: Cho ngũ giác ABCDE. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DE. I, J là trung điểm của MP, NQ. Chứng minh rằng: 
Cho tam giác ABC, gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Số vectơ bằng vectơ M N → có điểm đầu và điểm cuối trùng với một trong các điểm A, B, C, M, N, P bằng:
A. 1
B. 2
C. 3
D. 6
Cho tam giác ABC gọi điểm D nằm trên cạnh BC sao cho BD=2DC, E là trung điểm của AD. Một đường thẳng bất kì qua E và cắt các cạnh AB AC , lần lượt tại M N. Tính tỉ số AB/AM+2AC/AN
Cho hình thang OABC có M, N lần lượt là trung điểm của OB và OCa. Phân tích vectơ overrightarrow{AM} theo overrightarrow{OA} vàoverrightarrow{OB} b. Phân tích các vectơ overrightarrow{BN} , overrightarrow{MN} theo 2 vectơ overrightarrow{OB} vàoverrightarrow{OC}
Đọc tiếp
Cho hình thang OABC có M, N lần lượt là trung điểm của OB và OC
a. Phân tích vectơ \(\overrightarrow{AM}\) theo \(\overrightarrow{OA}\) và\(\overrightarrow{OB}\)
b. Phân tích các vectơ \(\overrightarrow{BN}\) , \(\overrightarrow{MN}\) theo 2 vectơ \(\overrightarrow{OB}\) và\(\overrightarrow{OC}\)
Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ . Tính vecto tổng
O
A
→
+
O
B
→
+
O
C
→
+
O
D
→
A. vecto AD B. Vecto BC C. Vecto DI D. Vecto 0
Đọc tiếp
Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ . Tính vecto tổng O A → + O B → + O C → + O D →
A. vecto AD
B. Vecto BC
C. Vecto DI
D. Vecto 0
Cho tam giác ABC gọi M,N,P lần lượt là trung điểm của các cạnh AB,AC,BC a) Tìm các vectơ cùng phương AM b) Tìm các vectơ cùng hướng MN c) Tìm các vectơ ngược hướng BC
cho tam giác ABC gọi M N P lần lượt là trung điểm của các cạnh BC, CA, AB. chứng minh vectoAM - NB = PC