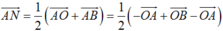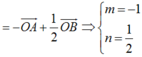Các câu hỏi tương tự
Cho tam giác OAB. Gọi M, N lần lượt là trung điểm của OA và OB. Tìm các số m, n sao cho:
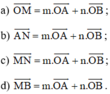
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm đối xứng với M qua N. Khi đó khẳng định nào sau đây đúng? A.
M
K
→
A
D
→
-
B
C
→
B.
M
K
→...
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD. K là điểm đối xứng với M qua N. Khi đó khẳng định nào sau đây đúng?
A. M K → = A D → - B C →
B. M K → = A D → + B C →
C. M K → = A B → - C D →
D. M K → = A C → - B D →
Nếu m, n là các số thực thỏa mãn
m
0
;
n
0
thì bất đẳng thức nào sau đây luôn đúng? A.
m
-
n
B.
n
-
m
0
C.
-
m
-
n
D.
m
-
n
0
Đọc tiếp
Nếu m, n là các số thực thỏa mãn m > 0 ; n < 0 thì bất đẳng thức nào sau đây luôn đúng?
A. m > - n
B. n - m < 0
C. - m > - n
D. m - n < 0
Gọi M; N lần lượt là trung điểm của các cạnh AB; AC của tam giác đều ABC. Đẳng thức nào sau đây đúng? A.
M
A
→
M
B
→
.
B.
A
B
→
A
C
→
.
C.
M...
Đọc tiếp
Gọi M; N lần lượt là trung điểm của các cạnh AB; AC của tam giác đều ABC. Đẳng thức nào sau đây đúng?
A. M A → = M B → .
B. A B → = A C → .
C. M N → = B C → .
D. B C → = 2 M N → .
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi O là giao điểm các đường chéo của tứ giác MNPQ, trung điểm các đoạn thẳng AC, BD tương ứng là I, J. Khẳng định nào sau đây đúng? A.
O
I
→
O
J
→
B.
O
A
→
...
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi O là giao điểm các đường chéo của tứ giác MNPQ, trung điểm các đoạn thẳng AC, BD tương ứng là I, J. Khẳng định nào sau đây đúng?
A. O I → = O J →
B. O A → = O C →
C. O B → = O D →
D. O I → = - O J →
Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của CM. Khẳng định nào sau đây là đúng? A.
A
N
→
1
2
A
B
→
+
2
3
A
C
→
B.
A...
Đọc tiếp
Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của CM. Khẳng định nào sau đây là đúng?
A. A N → = 1 2 A B → + 2 3 A C →
B. A N → = 3 4 A B → + 1 4 A C →
C. A N → = 1 4 A B → + 1 2 A C →
D. A N → = 1 3 A B → + 2 3 A C →
Cho tam giác ABC. M và N lần lượt thuộc hai tia AB và AC (M, N khác A). Khẳng định nào sau đây là đúng? A.
S
A
M
N
S
A
B
C
3
A
M
A
B
.
A...
Đọc tiếp
Cho tam giác ABC. M và N lần lượt thuộc hai tia AB và AC (M, N khác A). Khẳng định nào sau đây là đúng?
A. S A M N S A B C = 3 A M A B . A N A C
B. S A M N S A B C = 1 2 A M A B . A N A C
C. S A M N S A B C = 2 A M A B . A N A C
D. S A M N S A B C = A M A B . A N A C
Cho hình bình hành ABCD tâm O. Xác định vị trí điểm M thỏa mãn \(\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{AM}\). Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và dựng điểm K sao cho \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\). Khi đó, điểm K trùng với
Cho tam giác ABC. Các điểm M, N và P lần lượt là trung điểm của các cạnh AB, AC và BC.Đẳng thức nào sau đây đúng? A.
M
N
→
+
M
P
→
+
M
C
→
0
→
B.
P...
Đọc tiếp
Cho tam giác ABC. Các điểm M, N và P lần lượt là trung điểm của các cạnh AB, AC và BC.
Đẳng thức nào sau đây đúng?
A. M N → + M P → + M C → = 0 →
B. P M → + P N → = A M → + A N →
C. A M → + A N → - A P → = 0 →
D. A M → + A N → + M N → = 0 →