Vẽ tam giác ABC với B^ > C^. Quan sát hình và dự đoán xem ta có trường hợp nào trong các trường hợp sau:
1) AB = AC
2) AB > AC
3) AC > AB.
Vẽ tam giác ABC với AC > AB. Quan sát hình và dự đoán xem ta có trường hợp nào trong các trường hợp sau:
1) ∠B = ∠C
2) ∠B > ∠C
3) ∠B < ∠C
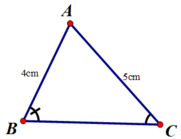
Ta vẽ ΔABC có AB = 4 cm; AC = 5 cm
Quan sát hình, ta dự đoán xảy ra trường hợp 2) ∠B > ∠C
Em hãy vẽ một tam giác ABC có AB = 3 cm, AC = 5 cm. Quan sát hình vừa vẽ và dự đoán xem trong hai góc B và C, góc nào lớn hơn.
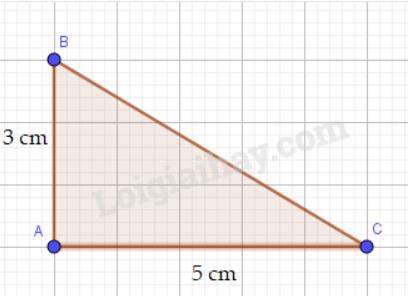
Dự đoán: Trong 2 góc B và C, góc B lớn hơn.
Quan sát tam giác ABC trong Hình 9.4
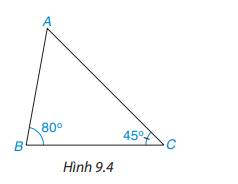
Em hãy dự đoán xem giữa hai cạnh đối diện với hai góc B và C ( tức là cạnh AC và AB) thì cạnh nào lớn hơn.
Em dự đoán cạnh đối diện với góc B lớn hơn cạnh đối diện với góc C.

Câu 1 : Cho tam tam giác ABC và tam giác DEF có C = F , B = E . Để tam giác ABC = tam giác DEF theo trường hợp cạnh - góc - cạnh cần trường hợp nào sau đây ?
A. AB = EF B. AC = DE C. BC = EF D . AB = DE
Câu 2 : Cho biết tam giác DEF = MNP . Khẳng định đúng là :
A. DE = PN B. E = N C. EF = MP D. E = M
cho tam giác ABC vuông tại A.Phân giác của 2 góc B và C cắt nhau tại I. Gọi D,E,F là các hình chiếu từ I xuống AB,AC,BC.
a) Chứng minh : AD = AE
b) Tính độ dài các đoạn AD và AE biết AB = 8cm ; AC = 15cm
c) Trong trường hợp tam giác ABC cân tại A. Chứng minh tam giác DEF cân
a: Xét ΔADI vuông tại D và ΔAEI vuông tại E có
AI chung
góc DAI=góc EAI
=>ΔADI=ΔAEI
=>AD=AE
b: BC=căn 8^2+15^2=17cm
P=(8+15+17)/2=20(cm)
S ABC=1/2*8*15=60cm2
=>AI=S/P=3cm
Xét tứ giác ADIE có
góc ADI=góc AEI=góc DAE=90 độ
AI là phân giác của góc DAE
=>ADIE là hình vuông
=>AD^2+AE^2=AI^2
=>2*AD^2=9
=>AD=3/căn 2
=>AE=3/căn 2
1. Cho ABC là tam giác vuông tại A. Tìm các tỉ số lượng giác của góc B trong các trường hợp sau:
a) BC = 5 cm; AB = 3 cm;
b) BC = 13 cm; AC = 12 cm;
c) BC = 5V2 cm; AB = 5 cm;
d) AB = a v3; AC = a.
d) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=\left(a\sqrt{3}\right)^2+a^2=4a^2\)
hay BC=2a
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{a}{2a}=\dfrac{1}{2}\)
\(\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{a\sqrt{3}}{2a}=\dfrac{\sqrt{3}}{2}\)
\(\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{a}{a\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
\(\cot\widehat{B}=\dfrac{AB}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Bài 1 Vẽ tam giác ABC vuông tại A,đường cao AH.Hãy tính BC,AH,BH,CH trong các trường hợp sau
1/ AB=7cm;AC/AB=2cm
2/AC=12cm;AC/AB=1cm
3/AC=3cm;AC/AB=√3cm
cho tam giác abc vuông tại A . tính tỉ số lượng giác của góc c trong các trường hợp sau a/ AC=8cm bc=17cm b/ ab=12cm Ac=12cm c/ AB=a BC=a√5
c: Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC=2a\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{a}{a\sqrt{5}}=\dfrac{\sqrt{5}}{5}\)
\(\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{2a}{a\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
\(\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{a}{2a}=\dfrac{1}{2}\)
\(\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{2a}{a}=2\)
1) cho tam giác ABC vuông tại a . tính bc VỚI trường hợp sau: 1)AB=3cm , AC=4cm . 2) AB=8, AC=6 . 3) AB=12 ,AC=16
1: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
2: \(BC=\sqrt{8^2+6^2}=10\left(cm\right)\)
3: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)