Cho hàm số f ( x ) = a 2 x 2 , x ≤ 2 , a ∈ ℝ ( 2 - a ) x 2 , x > 2 Giá trị của a để f (x) liên tục trên R là:
A. 1 và 2.
B. 1 và -1.
C. -1 và 2.
D. 1 và -2.
Những câu hỏi liên quan
SGK Cánh Diều
13 tháng 8 2023 lúc 22:35
Cho hàm số \(f(x) = {2^{3x + 2}}\)
a) Hàm số f(x) là hàm hợp của hàm số nào?
b) Tìm đạo hàm của f(x)
a) Hàm số f(x) là hàm hợp của hàm số \(y = {a^x}\)
b) \(f'(x) = \left( {{2^{3x + 2}}} \right)' = \left( {3x + 2} \right)'{.2^{3x + 2}}.\ln 2 = {3.2^{3x + 2}}.\ln 2\)
Đúng 0
Bình luận (0)
a) cho hàm số y=(f)x=x^6+1/x^3.cmr f(1/2)=f(x)
b) cho hàm số y=(f)x=x^2+1/x^2.CMR f(x)=f(-x)
c) cho hàm số y=(f)x=5^x. Tính f(x+1)-f(x)
HELPPPPPPPPPPPPP ME!
Cho hàm số y= F(x) = x×(x-2) và hàm số y= G(x) = -x+6
a) tính F(3); [ F(2/3) ]² ; G(-1/2)
b) tìm x để F(x)=0
c) tìm a để F(a)=G(a)
a: \(F\left(3\right)=3\left(3-2\right)=3\cdot1=3\)
\(\left[F\left(\dfrac{2}{3}\right)\right]^2=\left[\dfrac{2}{3}\cdot\left(\dfrac{2}{3}-2\right)\right]^2\)
\(=\left[\dfrac{2}{3}\cdot\dfrac{-4}{3}\right]^2=\left(-\dfrac{8}{9}\right)^2=\dfrac{64}{81}\)
\(G\left(-\dfrac{1}{2}\right)=-\left(-\dfrac{1}{2}\right)+6=6+\dfrac{1}{2}=\dfrac{13}{2}\)
b: F(x)=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
c: F(a)=G(a)
=>\(a\left(a-2\right)=-a+6\)
=>\(a^2-2a+a-6=0\)
=>\(a^2-a-6=0\)
=>(a-3)(a+2)=0
=>\(\left[{}\begin{matrix}a-3=0\\a+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=3\\a=-2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho hàm số f(x)=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
a) Tìm các g/trị của x để hàm số xác định
b) Tính f(\(4-2\sqrt{3}\)) và f(\(a^2\)) với a< -1
c) Tìm x sao cho f(x)=f(\(x^2\))
Câu 1:Cho hàm số y=f(x)=3x+1 a)Tính f (-2),f(1/2) b) Cho hàm số y=f (x)=5x Tính x khi y=20?
a: f(-2)=-6+1=-5
f(1/2)=3/2+1=5/2
Đúng 1
Bình luận (0)
Cho hàm số f(x)
tan
2
x
có nguyên hàm là F(x). Đồ thị hàm số y F(x) cắt trục tung tại điểm A(0; 2). Khi đó F(x) là A. F(x) tanx – x + 2. B. F(x) tanx + 2. C.
F
(
x
)
1
3
tan
3
x
+
2
D. F(x) cotx – x + 2.
Đọc tiếp
Cho hàm số f(x)= tan 2 x có nguyên hàm là F(x). Đồ thị hàm số y = F(x) cắt trục tung tại điểm A(0; 2). Khi đó F(x) là
A. F(x) = tanx – x + 2.
B. F(x) = tanx + 2.
C. F ( x ) = 1 3 tan 3 x + 2
D. F(x) = cotx – x + 2.
Chọn A.
F ( x ) = ∫ f ( x ) d x = ∫ tan 2 x d x = tan x - x + C
Vì đồ thị hàm số y = F(x) đi qua điểm A(0; 2) nên C = 2.
Vậy F(x) = tanx – x + 2.
Đúng 0
Bình luận (0)
cho hàm số y=1/2x
a.vẽ đồ thị hàm số trên
b.tính f(2), f(1), f(-2), f(-1), f(0)
c.tính giá trị của x khi f(x)=2 ,f(x)=1, f(x)=-1
d.những điểm nào sau đây thuộc đồ thị hàm số A(-1,1/2) B(-1,-1/2)
a: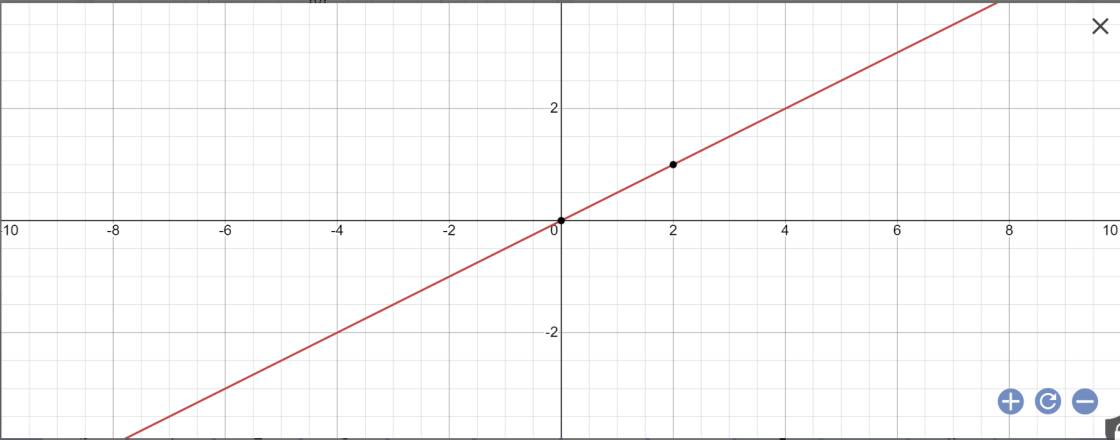 
b: \(f\left(2\right)=\dfrac{1}{2}\cdot2=1\)
\(f\left(1\right)=\dfrac{1}{2}\cdot1=\dfrac{1}{2}\)
\(f\left(-2\right)=\dfrac{1}{2}\cdot\left(-2\right)=-1\)
\(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\)
\(f\left(0\right)=\dfrac{1}{2}\cdot0=0\)
c: f(x)=2
=>\(\dfrac{1}{2}x=2\)
=>x=2*2=4
f(x)=1
=>\(\dfrac{1}{2}x=1\)
=>\(x=1:\dfrac{1}{2}=2\)
f(x)=-1
=>\(\dfrac{1}{2}x=-1\)
=>\(x=-1\cdot2=-2\)
d: \(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}\ne\dfrac{1}{2}=y_A\)
=>A(-1;1/2) không thuộc đồ thị hàm số y=1/2x
\(f\left(-1\right)=\dfrac{1}{2}\cdot\left(-1\right)=-\dfrac{1}{2}=y_B\)
=>\(B\left(-1;-\dfrac{1}{2}\right)\) thuộc đồ thị hàm số y=1/2x
Đúng 2
Bình luận (0)
Bài 1: Cho hàm số y =f( x)= -5x -1. Tính f(-1), f(0), f(1), f(1/2)
Bài 2: a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f(-1/2); f(1/2).
b) Cho hàm số y = g(x) = x – 1. Tính g(-1); g(0) ; g(1) ; g(2).
c) Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Lm giúp mình vs mình đang cần gấp .
Giải:
Bài 1: lần lượt thay các giá trị của x, ta có:
_Y=f(-1)= -5.(-1)-1=4
_Y=f(0)= -5.0-1=1
_Y=f(1)= -5.1-1=-6
_Y=f(1/2)= -5.1/2-1=-7/2
Đúng 1
Bình luận (1)
Bài 2:
a: f(-2)=7
f(-1)=5
f(0)=3
Đúng 1
Bình luận (1)
a, Cho hàm số y=f(x). Tính f(0);f(-1/3);f(5/2);f(a+b)
b, Cho hàm số y=g(x). Tính g(1);g(-1/2);g(-2);g(a-b)
. a) Cho hàm số y = f(x) = -2x + 3. Tính f(-2) ;f(-1) ; f(0) ; f( 1 2 ); f( 1 2 ). b) Cho hàm số y = g(x) = x 2 – 1. Tính g(-1); g(0
giúp e với ạ
a: f(-2)=4+3=7
f(-1)=2+3=5
f(0)=3
f(1/2)=-1+3=2
f(-1/2)=1+3=4
b: g(-1)=1-1=0
f(0)=0-1=-1
Đúng 0
Bình luận (0)