Chọn D.
Với ![]() ta có hàm số f(x) = a2x2 liên tục trên khoảng
ta có hàm số f(x) = a2x2 liên tục trên khoảng ![]() .
.
Với ![]() ta có hàm số f(x) = (2 – a)x2 liên tục trên khoảng
ta có hàm số f(x) = (2 – a)x2 liên tục trên khoảng ![]() .
.
Với ![]() ta có
ta có ![]() .
.
![]()
![]()
Để hàm số liên tục tại 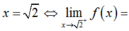
![]()
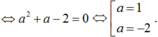
Vậy a = 1 hoặc a = -2 thì hàm số liên tục trên R.
Chọn D.
Với ![]() ta có hàm số f(x) = a2x2 liên tục trên khoảng
ta có hàm số f(x) = a2x2 liên tục trên khoảng ![]() .
.
Với ![]() ta có hàm số f(x) = (2 – a)x2 liên tục trên khoảng
ta có hàm số f(x) = (2 – a)x2 liên tục trên khoảng ![]() .
.
Với ![]() ta có
ta có ![]() .
.
![]()
![]()
Để hàm số liên tục tại 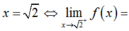
![]()
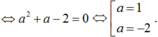
Vậy a = 1 hoặc a = -2 thì hàm số liên tục trên R.
Cho hàm số f ( x ) = a 2 x 2 , x ≤ 2 , a ∈ ℝ ( 2 - a ) x 2 , x > 2 . Giá trị của a để f(x) liên tục trên R là:
A. 1 và 2
B. 1 và -1
C. -1 và 2.
D. 1 và -2
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x - 1 ) 2 ( x 2 - 2 x ) với ∀ x ∈ ℝ . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số có 5 điểm cực trị?
A. 15
B. 17
C. 16
D. 18
Cho hàm số f ( x ) = a 2 x 2 x ≤ 2 , a ∈ R 2 - a x 2 x > 2 . Giá trị của a để f(x) liên tục
Cho hàm số y = f x = a x 5 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 . Biết f'(-1)=3 . Tính lim ∆ x → 0 f 1 + ∆ x - f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Cho hàm số: f x = 3 x - 5 v ớ i x ≤ - 2 a x - 1 v ớ i x > - 2
Với giá trị nào của a thì hàm số f(x) liên tục tại x=-2?
A. a=-5
B. a=0
C. a=5
D. a=6
Cho hàm số y = f x = 2 x 3 - 7 x + 6 x - 2 k h i x < 2 a + 1 - x 2 + x k h i x ≥ 2 . Xác định a để hàm số f(x) liên tục tại x = 2 .
Cho hàm số f ( x ) = sin 5 x 5 x x ≠ 0 a + 2 x = 0 . Tìm a để f(x) liên tục tại x = 0.
A. 1.
B. -1.
C. -2.
D. 2.
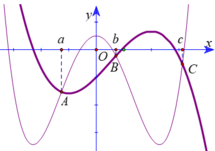
Cho hàm số y=f(x) và y=g(x) là hai hàm liên tục trên ℝ có đồ thị hàm số y = f '(x) là đường cong nét đậm và y = g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của y=f '(x) và y=g'(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) = f(x) - g(x) trên đoạn [a;c]?
![]()
![]()
![]()
![]()
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0