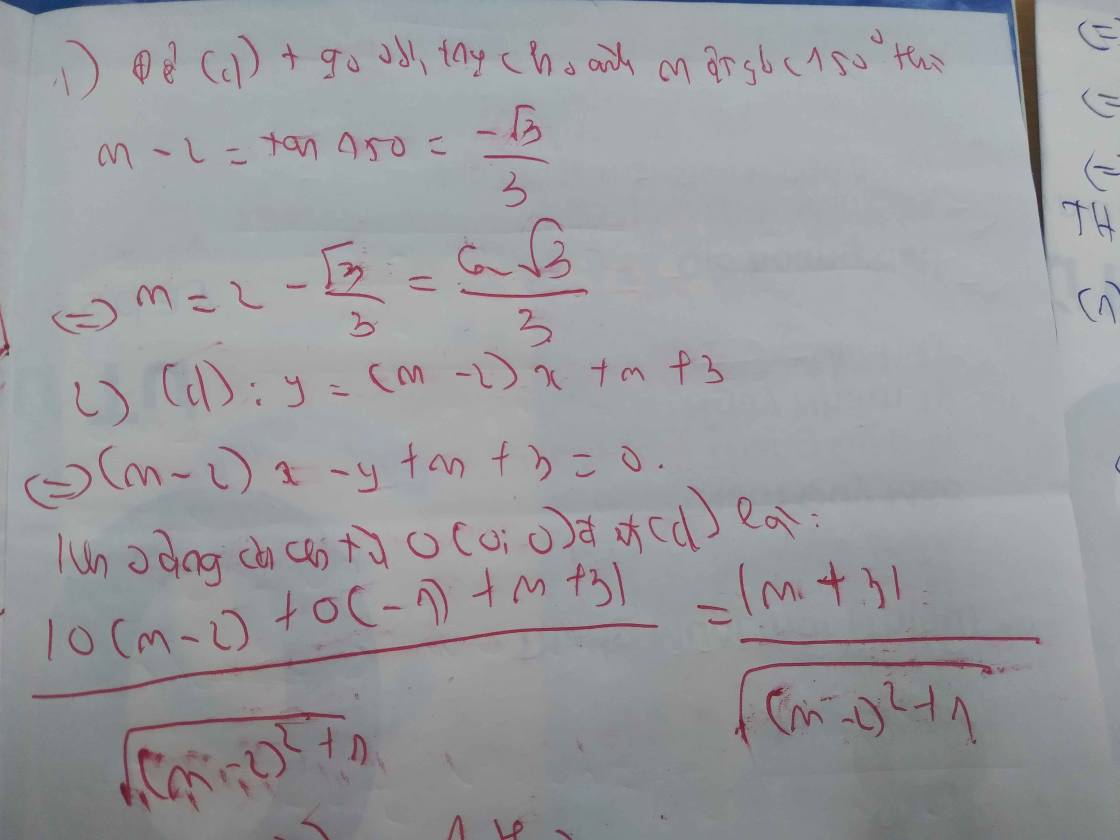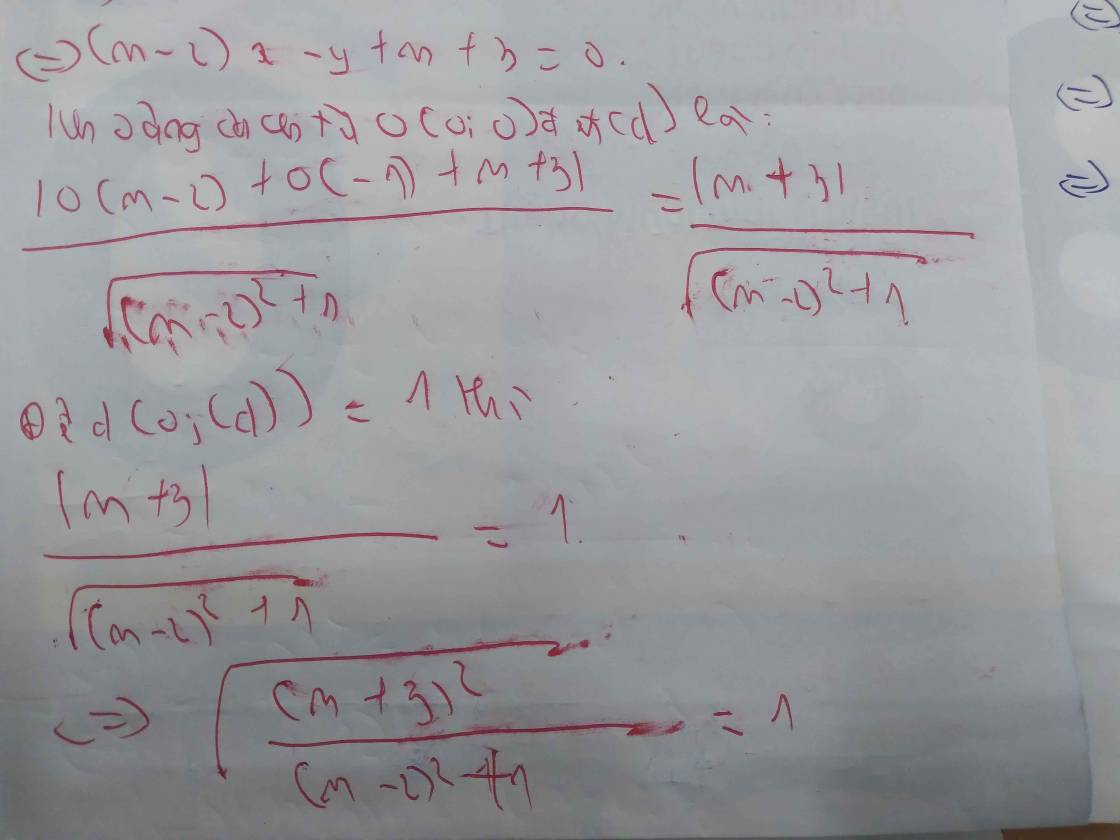Những câu hỏi liên quan
Cho đường thẳng y(m-2)x+m-3(d); m≠2. Tìm m biết:1) tìm m để hàm số đồng biến (tạo Ox góc nhọn), nghịch biến( tạo Ox góc tù)2) (d) đi qua A(1;2)3) (d) tạo với Ox góc 60 độ4) tìm m biết (d) cắt đường thẳng y2x-3 tại điểm có hoành độ bằng 35) cho m1. Vẽ đồ thị và tính khoảng cách từ O đến đường thẳng, gọi giao điểm của đồ thị với Ox và Oy là A và B. tính diện tích và chu vi tam giác AOB
Đọc tiếp
Cho đường thẳng y=(m-2)x+m-3(d); m≠2. Tìm m biết:
1) tìm m để hàm số đồng biến (tạo Ox góc nhọn), nghịch biến( tạo Ox góc tù)
2) (d) đi qua A(1;2)
3) (d) tạo với Ox góc 60 độ
4) tìm m biết (d) cắt đường thẳng y=2x-3 tại điểm có hoành độ bằng 3
5) cho m=1. Vẽ đồ thị và tính khoảng cách từ O đến đường thẳng, gọi giao điểm của đồ thị với Ox và Oy là A và B. tính diện tích và chu vi tam giác AOB
1-4 bạn tk ở đây: Cho đường thẳng y=(m-2)x+m-3(d); m≠2. Tìm m biết:1) tìm m để hàm số đồng biến (tạo Ox góc nhọn), nghịch biến( tạo Ox góc... - Hoc24
5. \(m=1\Leftrightarrow y=-x-2\)
PT giao Ox tại A và Oy tại B của đths: \(\left\{{}\begin{matrix}y=0\Rightarrow x=-2\Rightarrow A\left(-2;0\right)\Rightarrow OA=2\\x=0\Rightarrow y=-2\Rightarrow B\left(0;-2\right)\Rightarrow OB=2\end{matrix}\right.\)
Gọi H là chân đường cao từ O tới đths
Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\)
\(\Leftrightarrow OH^2=2\Leftrightarrow OH=\sqrt{2}\)
Vậy k/c từ O đến đt là \(\sqrt{2}\)
Áp dụng PTG: \(AB=\sqrt{OA^2+OB^2}=2\sqrt{2}\)
Vậy \(P_{ABC}=AB+BC+CA=4+2\sqrt{2};S_{ABC}=\dfrac{1}{2}OH\cdot AB=\dfrac{1}{2}\cdot2\sqrt{2}\cdot\sqrt{2}=2\left(đvdt\right)\)
Đúng 2
Bình luận (1)
Cho đường thẳng y(m-2)x+m-3(d); m≠2. Tìm m biết:1) tìm m để hàm số đồng biến (tạo Ox góc nhọn), nghịch biến( tạo Ox góc tù)2) (d) đi qua A(1;2)3) (d) tạo với Ox góc 60 độ4) tìm m biết (d) cắt đường thẳng y2x-3 tại điểm có hoành độ bằng 35) cho m1. Vẽ đồ thị và tính khoảng cách từ O đến đường thẳng, gọi giao điểm của đồ thị với Ox và Oy là A và B. tính diện tích và chu vi tam giác AOB6) tìm điểm cố định mà (d) luôn đi qua7) tìm m để (d) cắt đường thẳng y2x-1 tại một điểm trên trục tung
Đọc tiếp
Cho đường thẳng y=(m-2)x+m-3(d); m≠2. Tìm m biết:
1) tìm m để hàm số đồng biến (tạo Ox góc nhọn), nghịch biến( tạo Ox góc tù)
2) (d) đi qua A(1;2)
3) (d) tạo với Ox góc 60 độ
4) tìm m biết (d) cắt đường thẳng y=2x-3 tại điểm có hoành độ bằng 3
5) cho m=1. Vẽ đồ thị và tính khoảng cách từ O đến đường thẳng, gọi giao điểm của đồ thị với Ox và Oy là A và B. tính diện tích và chu vi tam giác AOB
6) tìm điểm cố định mà (d) luôn đi qua
7) tìm m để (d) cắt đường thẳng y=2x-1 tại một điểm trên trục tung
Cho đường thẳng y=(m-2)x+m-3(d); m≠2. Tìm m biết:
1) tìm m để hàm số đồng biến (tạo Ox góc nhọn), nghịch biến( tạo Ox góc tù)
2) (d) đi qua A(1;2)
3) (d) tạo với Ox góc 60 độ
4) tìm m biết (d) cắt đường thẳng y=2x-3 tại điểm có hoành độ bằng 3
\(1,\) Nhọn \(\Leftrightarrow m-2>0\Leftrightarrow m>2\)
Tù \(\Leftrightarrow m-2< 0\Leftrightarrow m< 2\)
\(2,\Leftrightarrow m-2+m-3=2\Leftrightarrow2m-5=2\Leftrightarrow m=\dfrac{7}{2}\)
\(3,\) PT giao Ox tại B và Oy tại C là \(\left\{{}\begin{matrix}y=0\Rightarrow\left(m-2\right)x=3-m\Rightarrow x=\dfrac{3-m}{m-2}\Rightarrow A\left(\dfrac{3-m}{m-2};0\right)\Rightarrow OA=\left|\dfrac{3-m}{m-2}\right|\\x=0\Rightarrow y=m-3\Rightarrow B\left(0;m-3\right)\Rightarrow OB=\left|m-3\right|\end{matrix}\right.\)
(d) tạo với Ox góc 60 độ là góc nhọn \(\Leftrightarrow m-2>0\Leftrightarrow m>2\)
Và \(\tan60^0=\dfrac{OB}{OA}=\left|m-3\right|\cdot\dfrac{\left|m-2\right|}{\left|3-m\right|}=\left|\dfrac{\left(m-3\right)\left(2-m\right)}{m-3}\right|=\left|2-m\right|\)
\(\Leftrightarrow\left|2-m\right|=\sqrt{3}\)
Mà \(m>2\Leftrightarrow2-m< 0\Leftrightarrow2-m=-\sqrt{3}\Leftrightarrow m=2+\sqrt{3}\)
\(4,\) PT hoành độ giao điểm tại hoành độ 3:
\(\left(m-2\right)x+m-3=2x-3\)
Thay \(x=3\Leftrightarrow3m-6+m-3=3\)
\(\Leftrightarrow4m=12\Leftrightarrow m=3\)
Đúng 2
Bình luận (0)
Cho hàm số bậc nhất y = (2m + 1)x + m – 2. Tìm m biết rằng góc tạo bởi đường thẳng và trục Ox bằng 45 ° .
A. m = 0
B. m = 1
C. m = -1
D. m = 2
Đáp án A
Vì hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0 ⇔ m ≠ (-1)/2 .
Gọi góc α là góc tạo bởi đường thẳng và trục Ox . Theo giả thiết α = 45 ° . Ta có:
tan α = a ⇒ tan45 ° = 2m + 1
⇔ 1 = 2m + 1 ⇔ 0 = 2m ⇔ m = 0
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y-2x -5 (d) và y -x (d)
A. Vẽ đồ thị d và d của 2 hàm số đã cho trêb cùng 1 hệ tọa đọi Oxy
B. Tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ ( bằng phép tính)
C. Tính góc alpha tạo bởi đường thẳng d với trục hoành Ox ( làm tròn kết quả đến độ)
D. Gọi giao điểm của d với trục Oy là A, tính chu vi và diện tích tam giác MOA ( đơn vị đo trên các trục tọa độ là cm)
Đọc tiếp
Cho hàm số bậc nhất y=-2x -5 (d) và y= -x (d') A. Vẽ đồ thị d và d' của 2 hàm số đã cho trêb cùng 1 hệ tọa đọi Oxy B. Tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ ( bằng phép tính) C. Tính góc alpha tạo bởi đường thẳng d với trục hoành Ox ( làm tròn kết quả đến độ) D. Gọi giao điểm của d với trục Oy là A, tính chu vi và diện tích tam giác MOA ( đơn vị đo trên các trục tọa độ là cm)
a) \(\left\{{}\begin{matrix}\left(d\right):y=-2x-5\\\left(d'\right):y=-x\end{matrix}\right.\)
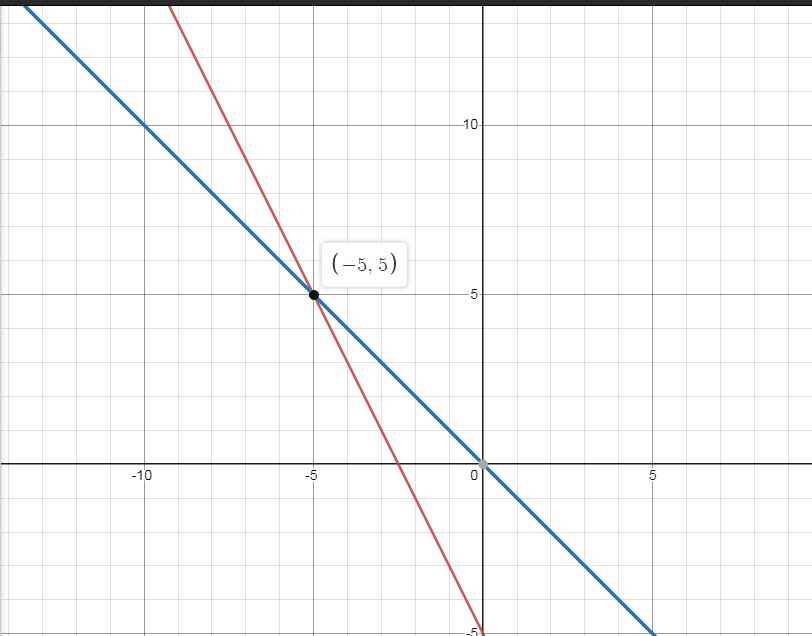
b) \(\left(d\right)\cap\left(d'\right)=M\left(x;y\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)
\(\Rightarrow M\left(-5;5\right)\)
c) Gọi \(\widehat{M}=sđ\left(d;d'\right)\)
\(\left(d\right):y=-2x-5\Rightarrow k_1-2\)
\(\left(d'\right):y=-x\Rightarrow k_1-1\)
\(tan\widehat{M}=\left|\dfrac{k_1-k_2}{1+k_1.k_2}\right|=\left|\dfrac{-2+1}{1+\left(-2\right).\left(-1\right)}\right|=\dfrac{1}{3}\)
\(\Rightarrow\widehat{M}\sim18^o\)
Đúng 0
Bình luận (0)
d) \(\left(d\right)\cap Oy=A\left(0;y\right)\)
\(\Leftrightarrow y=-2.0-5=-5\)
\(\Rightarrow A\left(0;-5\right)\)
\(OA=\sqrt[]{0^2+\left(-5\right)^2}=5\left(cm\right)\)
\(OM=\sqrt[]{5^2+5^2}=5\sqrt[]{2}\left(cm\right)\)
\(MA=\sqrt[]{5^2+10^2}=5\sqrt[]{5}\left(cm\right)\)
Chu vi \(\Delta MOA:\)
\(C=OA+OB+MA=5+5\sqrt[]{2}+5\sqrt[]{5}=5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)\left(cm\right)\)
\(\Rightarrow p=\dfrac{C}{2}=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}p-OA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5=\dfrac{5\left(\sqrt[]{2}+\sqrt[]{5}-1\right)}{2}\\p-OB=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{2}=\dfrac{5\left(-\sqrt[]{2}+\sqrt[]{5}+1\right)}{2}\\p-MA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{5}=\dfrac{5\left(\sqrt[]{2}-\sqrt[]{5}+1\right)}{2}\end{matrix}\right.\)
\(p\left(p-MA\right)=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}.\dfrac{5\left(1+\sqrt[]{2}-\sqrt[]{5}\right)}{2}\)
\(\Leftrightarrow p\left(p-MA\right)=\dfrac{25\left[\left(1+\sqrt[]{2}\right)^2-5\right]}{4}=\dfrac{25.2\left(\sqrt[]{2}-1\right)}{4}=\dfrac{25\left(\sqrt[]{2}-1\right)}{2}\)
\(\left(p-OA\right)\left(p-OB\right)=\dfrac{25\left[5-\left(\sqrt[]{2}-1\right)^2\right]}{4}\)
\(\Leftrightarrow\left(p-OA\right)\left(p-OB\right)=\dfrac{25.2\left(\sqrt[]{2}+1\right)}{4}=\dfrac{25\left(\sqrt[]{2}+1\right)}{4}\)
Diện tích \(\Delta MOA:\)
\(S=\sqrt[]{p\left(p-OA\right)\left(p-OB\right)\left(p-MA\right)}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25\left(\sqrt[]{2}-1\right)}{2}.\dfrac{25\left(\sqrt[]{2}+1\right)}{2}}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25^2}{2^2}}=\dfrac{25}{2}=12,5\left(cm^2\right)\)
Đúng 0
Bình luận (0)
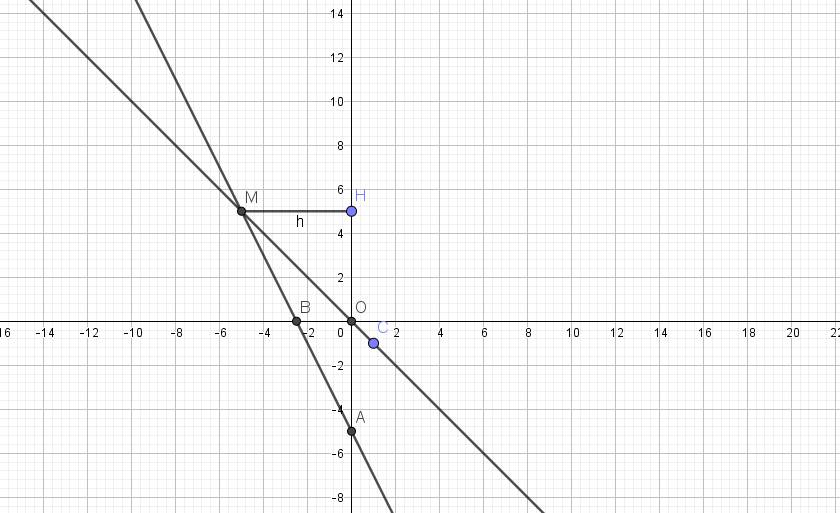
| x | 0 | -5/2 | 1 |
| y=-2x-5 | -5 | 0 | |
| y=-x | 0 | -1 |
*) Đồ thị:
b) Phương trình hoành độ giao điểm của (d) và (d'):
\(-2x-5=-x\)
\(\Leftrightarrow-2x+x=5\)
\(\Leftrightarrow x=-5\) \(\Rightarrow y=-\left(-5\right)=5\)
Vậy tọa độ giao điểm của (d) và (d') là \(M\left(-5;5\right)\)
c) Ta có:
\(tanB=\dfrac{OA}{OB}=\dfrac{-5}{-\dfrac{5}{2}}=2\)
\(\Rightarrow\widehat{B}\simeq63^0\)
Mà góc tạo bởi d với trục hoành là \(\widehat{OBM}\)
\(\Rightarrow\widehat{OBM}\simeq180^0-63^0=117^0\)
d) Ta có:
\(OM^2=5^2+5^2=50\)
\(\Rightarrow OM=5\sqrt{2}\left(cm\right)\)
\(AM^2=5^2+10^2=125\)
\(\Rightarrow AM=5\sqrt{5}\left(cm\right)\)
Chu vi \(\Delta MOA\):
\(5\sqrt{2}+5\sqrt{5}+5=5\left(\sqrt{2}+\sqrt{5}+1\right)\left(cm\right)\)
Diện tích \(\Delta MOA\)
\(S_{MOA}=\dfrac{MH.OA}{2}=\dfrac{5.5}{2}=25\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Bài II (2.5 điểm): Cho hàm số bậc nhất y (m - 1) x +m có đồ thị là đường thẳng (d) với m khác 11. Với m2, vẽ đồ thị hàm số và tính số đo góc tạo bởi đường thẳng (d) và trục Ox (làm tròn đến độ)2. Tìm m để đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 13. Tìm điểm cố định mà đường thẳng (d) luôn đi qua với mọi giá trị của mEm cần gấp ạ
Đọc tiếp
Bài II (2.5 điểm): Cho hàm số bậc nhất y = (m - 1) x +m có đồ thị là đường thẳng (d) với m khác 1
1. Với m=2, vẽ đồ thị hàm số và tính số đo góc tạo bởi đường thẳng (d) và trục Ox (làm tròn đến độ)
2. Tìm m để đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 1
3. Tìm điểm cố định mà đường thẳng (d) luôn đi qua với mọi giá trị của m
Em cần gấp ạ
1: Khi m=2 thì y=(2-1)x+2=x+2
Vẽ đồ thị:
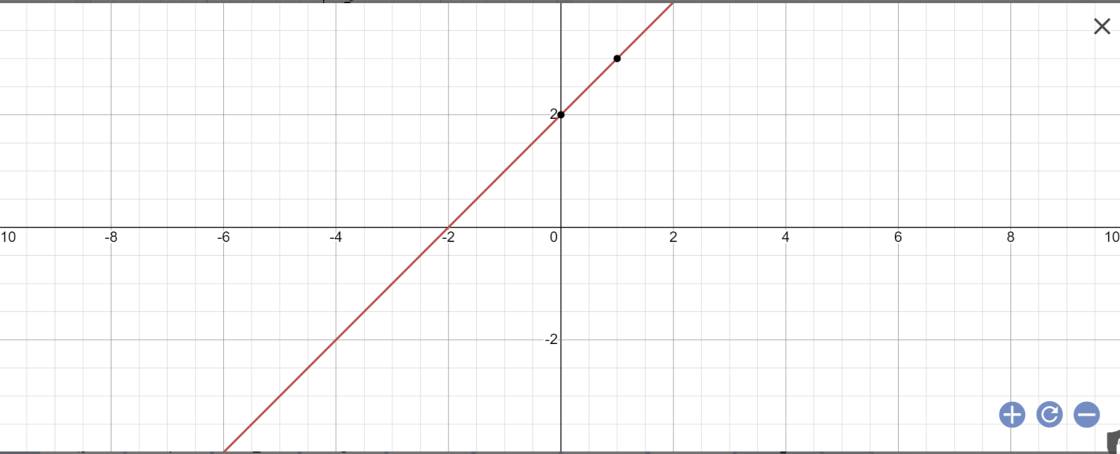
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
2: Thay x=1 và y=0 vào (d), ta được:
\(1\left(m-1\right)+m=0\)
=>2m-1=0
=>m=1/2
3:
y=(m-1)x+m
=mx-x+m
=m(x+1)-x
Điểm mà (d) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}x+1=0\\y=-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho các hàm số: y = (m - 1)x + 2m – 5 (1)
y = (3 – 2m)x + m – 8 (2)
Tìm m để góc tạo bởi đồ thị hàm số (1) với Ox là
60o
. Tìm m để góc tạo bởi đồ thị hàm số (2) với Ox là
120o
.
Ta có : tg60=m-1
\({\sqrt{3}=m-1} \) \(->m=\sqrt{3} +1\)
\(tan120=3-2m <=> -\sqrt{3}=3-2m \)
m=\(\frac{3+\sqrt{3}}{2}\)
Đúng 0
Bình luận (0)
Bài 1: Cho hàm số bậc nhất y=(m-1)x+2
a)Tìm m để (d)tạo với Ox một góc nhọn
b)Tìm m để (d)đi qua A (2,5)
c)TÌm tọa độ giảo điểm A,B của (d) với Ox ,Oy
d)Tìm m để tam giác ABC vuông cân
Cho hàm số bậc nhất y(m-2)x+m+3 (d) (m ≠ 2)1) Tìm m biết (d) tạo với trục hoành 1 góc 150o2) tìm m dể khảng cách từ gốc tọa độ đến đường thẳng (d) 13) tìm m để (d) cắt Ox,Oy tạo thành tam giác có diện tích 2giúp mik giải bài này vs mik đag cần gấp
Đọc tiếp
Cho hàm số bậc nhất y=(m-2)x+m+3 (d) (m ≠ 2)
1) Tìm m biết (d) tạo với trục hoành 1 góc 150o
2) tìm m dể khảng cách từ gốc tọa độ đến đường thẳng (d) =1
3) tìm m để (d) cắt Ox,Oy tạo thành tam giác có diện tích =2
giúp mik giải bài này vs![]()
![]() mik đag cần gấp
mik đag cần gấp