Cho cấp số nhân (un) với u 1 = − 1 ; q = − 1 10 . Số 1 10 103 là số hạng thứ mấy của (un) ?
A. Số hạng thứ 103
B. Số hạng thứ 104
C. Số hạng thứ 105
D. Đáp án khác
Cho dãy số (un) với un = 3.2n (n ≥ 1). Dãy (un) có là cấp số nhân không? Vì sao?
Ta có: un+1 = 3.2n+1
\( \Rightarrow \frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{{{3.2}^{n + 1}}}}{{{{3.2}^n}}} = 2\) với n ≥ 1
Vì vậy dãy (un) là cấp số nhân có số hạng đầu u1 = 6 và công bội q = 2.
Cho cấp số nhân u n với u 1 = - 1 ; q = 0 , 00001 . Tìm q và u n ?
A. q = 1 10 ; u n = - 1 10 n - 1
B. q = - 1 10 ; u n = - 10 n - 1
C. q = - 1 10 ; u n = 1 10 n - 1
D. q = - 1 10 ; u n = - 1 n 10 n - 1
Cho cấp số nhân u n với u 1 = - 1 ; q = - 1 10 . Số 1 10 103 là số hạng thứ mấy của u n
A. Số hạng thứ 103
B. Số hạng thứ 104
C. Số hạng thứ 105
D. Không là số hạng của cấp số đã cho
Cho cấp số nhân ( u n ) có u n = 2 ( - 3 ) n + 1 . Tìm công bội q của cấp số nhân đó
A. q = 6 ( 3 + 1 )
B. q = - 6 ( 3 + 1 )
C. q = 3
D. q = - 3
Cho dãy số ( u n ) : u 1 = 0 u n + 1 = 2 u n + 3 u n + 4 v ớ i n ≥ 1
a) Lập dãy số ( x n ) với x n = u n - 1 u n + 3 . Chứng minh dãy số là cấp số nhân.
b) Tìm công thức tính x n , u n theo n.
Cho cấp số nhân (un), với u1=1 và công bội q=\(\dfrac{1}{2}\).
a) So sánh |q| với 1.
b) Tính Sn=u1+u2+...+un.. Từ đó, hãy tính limSn.
a: |q|=1/2<1
b: Sn=U1+u2+...+un
\(S_n=\dfrac{1\left(1-\left(\dfrac{1}{2}\right)^n\right)}{1-\dfrac{1}{2}}=2\left(1-\left(\dfrac{1}{2}\right)^n\right)\)
=>\(lim\left(S_n\right)=2\)
Cho cấp số nhân u 1 , u 2 , u 3 , .. u n với công bội q q ≠ 0 , q ≠ 1 . Đặt S n = u 1 + u 2 + u 3 + .. + u n . Khi đó ta có:
A. S n = u 1 q n − 1 q − 1
B. S n = u 1 q n − 1 − 1 q − 1
C. S n = u 1 q n + 1 q + 1
D. S n = u 1 q n − 1 − 1 q + 1
Chọn A.
Phương pháp:
Sử dụng công thức tính tổng của n số hạng đầu của cấp số nhân có số hạng đầu tiên là
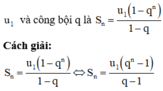
Cho cấp số nhân u n , biết u 1 = 1 ; u 4 = 64 . Tính công bội q của cấp số nhân
A. q =4
B. q = 2 2
C. q =21.
D. q = ± 4 .
Đáp án A
Theo công thức tổng quát của cấp số nhân
![]()
Cho cấp số nhân ( u n ) , biết u 1 = 1 ; u 4 = 64 . Tính công bội q của cấp số nhân.
A. q = 4 .
B. q = 2 2 .
C. q = 21 .
D. q = ± 4 .
Chọn A
Theo công thức tổng quát của cấp số nhân
![]()