Tập xác định của hàm số y = 1 sin x - cos x là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tập xác định của các hàm số sau:
a) \(y = \frac{{1 - \cos x}}{{\sin x}}\);
b) \(y = \sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} .\)
a) Biểu thức \(\frac{{1 - \cos x}}{{\sin x}}\) có nghĩa khi \(\sin x \ne 0\), tức là \(x \ne k\pi \;\left( {k\; \in \;\mathbb{Z}} \right)\).
Vậy tập xác định của hàm số đã cho là \(\mathbb{R}/{\rm{\{ }}k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}\} \;\)
b) Biểu thức \(\sqrt {\frac{{1 + \cos x}}{{2 - \cos x}}} \) có nghĩa khi \(\left\{ {\begin{array}{*{20}{c}}{\frac{{1 + \cos x}}{{2 - \cos x}} \ge 0}\\{2 - \cos x \ne 0}\end{array}} \right.\)
Vì \( - 1 \le \cos x \le 1 ,\forall x \in \mathbb{R}\)
Vậy tập xác định của hàm số là \(D = \mathbb{R}\)
Trong các hàm số sau, có bao nhiêu hàm số là hàm chẵn trên tập xác định của nó?
y = cot 2x; y = cos(x + π); y = 1 – sin x; y = tan2016x
A. 1.
B. 2
C. 3
D. 4
Đáp án B
+ Xét hàm y = f(x) = cos (x + π)
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-x + π) = -cos x = cos (x + π) = f(x)
Do đó y = cos (x + π) là hàm số chẵn .
+ Xét hàm y = g(x) = tan2016x
TXĐ: D = R\{π/2 + kπ, k ∈ Z}
Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = tan2016(-x) = (-tan x)2016 = tan2016x = g(x)
Do đó: y = tan2016x là hàm chẵn trên tập xác định của nó.
+Xét hàm y = cot2x
f(-x) = cot(-2x) = - cot 2x = -f(x) nên đây là hàm số lẻ.
+ Xét hàm số y = 1-sinx
f(-x) = 1- sin(-x) = 1+ sin x
Nên hàm số không chẵn không lẻ
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Khẳng định nào sau đây là sai?
A. Hàm số \(y = \cos x\) có tập xác định là \(\mathbb{R}\)
B. Hàm số \(y = \cos x\) có tập giá trị là [-1;1]
C. Hàm số \(y = \cos x\) là hàm số lẻ
D. Hàm số \(y = \cos x\) tuần hoàn với chu kỳ \(2\pi \)
Ta có: \(y = \cos x\)
\(y\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = y\)
Suy ra hàm số \(y = \cos x\) là hàm số chẵn
Vậy ta chọn đáp án C
Tập xác định của hàm số y = 1 + cos x 1 - cos x là:
![]()
![]()
![]()
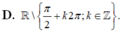
Tập xác định của hàm số \(y = \frac{{\cos x}}{{\sin x - 1}}\) là
A. \(\mathbb{R}\backslash \{ k2\pi {\rm{|}}k\; \in \;\mathbb{Z}{\rm{\} }}\)
B. \(\mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k2\pi {\rm{|}}k\; \in \;\mathbb{Z}} \right\}\)
C. \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}k\; \in \;\mathbb{Z}} \right\}\)
D. \(\mathbb{R}\backslash \{ k\pi {\rm{|}}k\; \in \;\mathbb{Z}{\rm{\} }}\)
Hàm số xác định khi: \(\sin x - 1\; \ne 0\; \Leftrightarrow \sin x \ne 1\; \Leftrightarrow x \ne \frac{\pi }{2} + k2\pi ,\;\;k \in \mathbb{Z}\)
Vậy ta chọn đáp án B
1.Tìm tập xác định của hàm số: y= \(\sqrt{1+sinx-2cos^2x}\)
2. Cho hàm số: y = \(\sqrt{sin^4x+cos^4x-2msinx.cosx}\)
Tìm các giá trị của m để xác định với mọi x.
Tập xác định của hàm số y = 1 - cos x sin x - 1 là
![]()
![]()
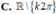
![]()
Tập xác định của hàm số y = 1 - cos x sin x - 1 là:
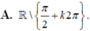
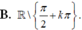
![]()
![]()
tìm tập xác định của mỗi hàm số sau : a) y = \(\sqrt{\frac{1-\sin x}{1+\cos x}}\) ; b) y = \(\tan\left(2x+\frac{\pi}{3}\right)\).
a)\(\forall x\Rightarrow sinx\le1\Rightarrow1-sinx\ge0\)
cosx\(\ge-1\Rightarrow1+cosx\ge0\)
ĐK:cosx\(\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
\(\Rightarrow D=\left\{R\backslash\left\{\pi+k2\pi\right\}\right\}\)
b)ĐK:\(cos\left(2x+\frac{\pi}{3}\right)\ne0\Leftrightarrow2x+\frac{\pi}{3}\ne\frac{\pi}{2}+k\pi\Leftrightarrow x\ne\frac{\pi}{12}+\frac{k\pi}{2}\)
\(\Rightarrow D=\left\{R\text{\}\left\{\frac{\pi}{12}+\frac{k\pi}{2}\right\}\right\}\)