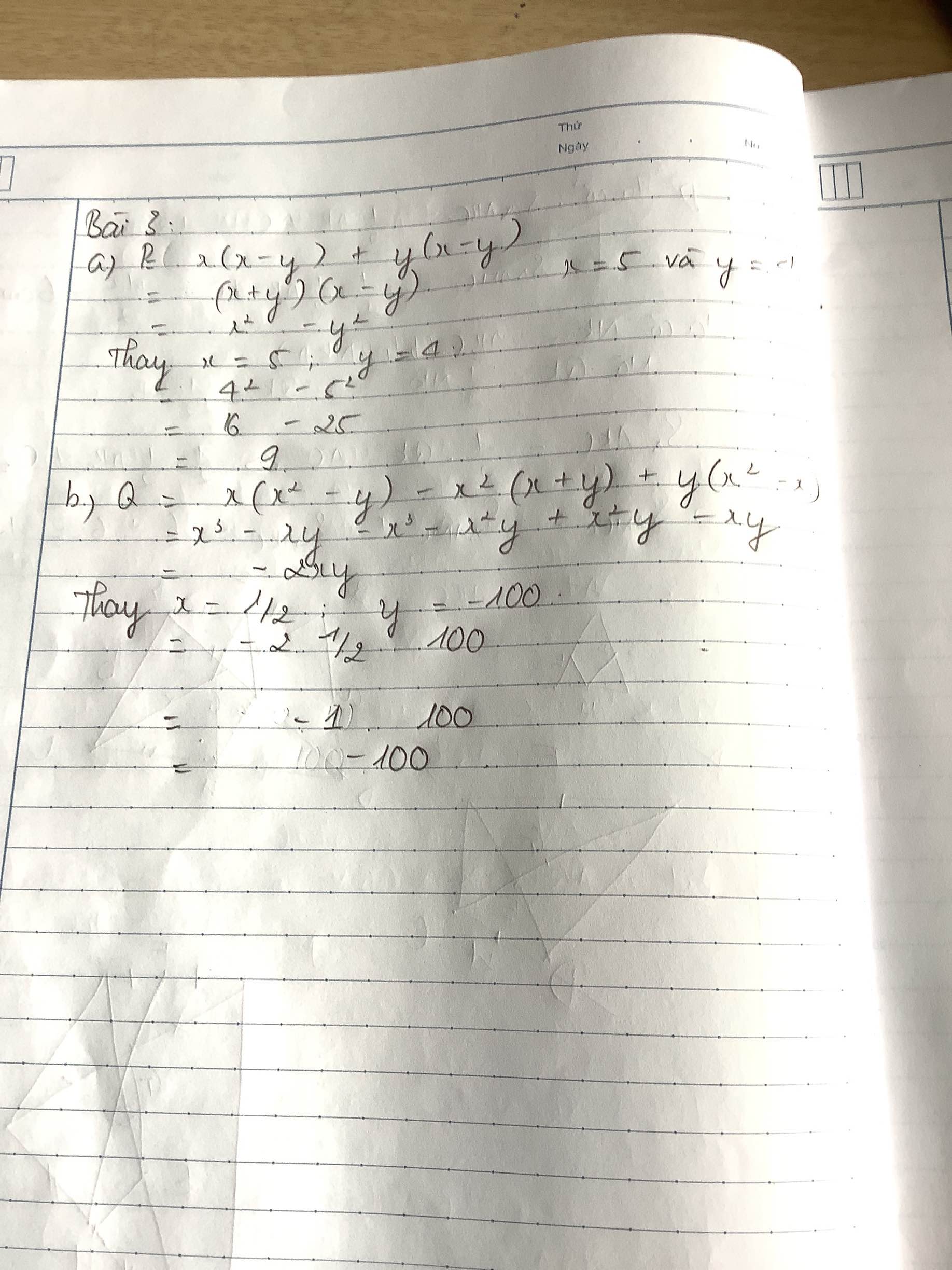Tính giá trị của biểu thức: x2 + 4x + 4 tại x = 98.

Những câu hỏi liên quan
Tính giá trị của biểu thức B = x 3 + x 2 - 6 x x 3 - 4 x với x = 98
Điều kiện xác định của phân thức: x ≠ 0, x ≠ -2, x ≠ 2
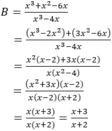
Ta có x = 98 thỏa mãn ĐKXĐ của biến nên thay x = 98 vào phân thức  ta được
ta được
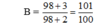
Đúng 0
Bình luận (0)
Tính giá trị biểu thức B=x + 4x + 4 Tại x =98
\(B=x^2+4x+4=\left(x+2\right)^2\)
Thay x=98 vào B ta có:
\(B=x^2+4x+4=\left(x+2\right)^2=\left(98+2\right)^2=100^2=10000\)
Đúng 2
Bình luận (1)
\(B=x^2+4x+4=\left(x+2\right)^2=\left(98+2\right)^2=100^2=10000\)
Đúng 2
Bình luận (1)
B=x2+4x+4
B=(x+2)2
thay: x=98
có:B=(98+2)2=10000
Đúng 0
Bình luận (1)
Tính giá trị của biểu thức
A
x
3
+
3
x
(
x
+
1
)
+
1
3
−
x
2
−
4
x
+
4
t
ạ
i
x
2017
3...
Đọc tiếp
Tính giá trị của biểu thức A = x 3 + 3 x ( x + 1 ) + 1 3 − x 2 − 4 x + 4 t ạ i x = 2017 3 .
Ta có A = x 3 + 3 x ( x + 1 ) + 1 3 − x 2 − 4 x + 4 = x + 1 − x − 2 .
A= 3 với x ≥ 2. Do đó A= 3 khi x = 2017 3 .
Đúng 0
Bình luận (0)
tính giá trị của biểu thức
a) x^2 +4x + 4 tại x= 98
b) x^3 + 3x^2 +3x+ 1 tại x= 99
a) Thay x = 98 vào biểu thức ta được:
982 + 4.98 + 4
= 982 + 2.2.98 + 22
= ( 98 + 2)2
= 1002 = 10000
b) Thay x= 99 vào biểu thức ta được:
993 +3.992 + 3.99 +1
= 993 + 3.992.1 + 3.99.12 +13
= ( 99 + 1)3
= 1003 = 1000000
Đúng 0
Bình luận (0)
Tính giá trị của biểu thức
Xem chi tiết
a) x^2 + 4x + 4 tại x =98
b) x^3 +3x^2 + 3x + 1 tại x =99
Cho biểu thức A=x2-4x+4/5x-10
a) Với điều kiện nào của x thì giá trị biểu thức của A được xác định
b) Rút gọn biểu thức A
c) Tìm giá trị của biểu thức A tại x=-2018
a) \(A=\dfrac{x^2-4x+4}{5x-10}.\) ĐK: \(x\ne2.\)
b) \(A=\dfrac{x^2-4x+4}{5x-10}=\dfrac{\left(x-2\right)^2}{5\left(x-2\right)}=\dfrac{x-2}{5}.\)
c) \(Thay\) \(x=-2018:\) \(\dfrac{-2018-2}{5}=-404.\)
Đúng 1
Bình luận (0)
Tính giá trị của biểu thức tại x=3
A=(x-1)x2-4x(x-1)+4x(x-1)
Vì x=3
A=(x-1)2x-4x(x-1)+4x(x-1)
A=(x-1)2x
A=2x2-2x
A=2x(x-1)
A=2.3(3-1)
A=12
tớ thu gọn luôn -4x với +4x nên =0 cậu ak
Đúng 0
Bình luận (0)
tính giá trị của biểu thức
a) x2-2x+1 tại x=-1/1
b)4x2+4x+1 tại x=1/2
a: A=(x-1)^2=(-1-1)^2=4
b: B=(2x+1)^2=2^2=4
Đúng 0
Bình luận (0)
Bài 3:
a) Tính giá trị của biểu thức tại P = x(x - y) + y(x - y) tại x = 5 và y = 4;
b) Tính giá trị của biểu thức tại Q = x(x2 - y) - x2(x + y) + y(x2 - x) tại x = 1/2 và y = -100;
a) \(P=x\left(x-y\right)+y\left(x-y\right)=\left(x-y\right)\left(x+y\right)=x^2-y^2=5^2-4^2=9\)
b) \(Q=x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)=x^3-xy-x^3-x^2y+x^2y-xy=0\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời