Hãy chứng minh rằng khoảng cách từ một hành tinh đến mặt trời thì tỉ lệ nghịch với căn bậc hai của vận tốc của hành tinh đó tại một vị trí trên quỹ đạo R 1 R 2 = v 2 v 1

Những câu hỏi liên quan
Một vệ tinh nhân tạo địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất một khoảng 7200km , tâm quỹ đạo vệ tinh trùng với tâm O của Trái Đất. Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một vị trí trên mặt đất.
a) Hỏi vị trí xa nhất trên Trái Đất có thể nhận được tín hiệu từ vệ tinh này cách vệ tinh một khoảng bao nhiêu km? Biết Trái Đất được xem như một hình cầu có bán kính khoảng 6400km.
b) Hãy tính độ lớn nhất của góc mà từ vệ tinh có thể truyền được tín hiệu đến Trái Đất (...
Đọc tiếp
Một vệ tinh nhân tạo địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất một khoảng 7200km , tâm quỹ đạo vệ tinh trùng với tâm O của Trái Đất. Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một vị trí trên mặt đất.
a) Hỏi vị trí xa nhất trên Trái Đất có thể nhận được tín hiệu từ vệ tinh này cách vệ tinh một khoảng bao nhiêu km? Biết Trái Đất được xem như một hình cầu có bán kính khoảng 6400km.
b) Hãy tính độ lớn nhất của góc mà từ vệ tinh có thể truyền được tín hiệu đến Trái Đất (xem hình vẽ).
- A: Vị trí của vệ tinh.
- AB, AC: các tiếp tuyến của đường tròn (O).
- Hai tiếp điểm B, C: vị trí xa nhất trên Trái Đất có thể nhận được tín hiệu từ vệ tinh.
- AH: độ cao của vệ tinh.
- Góc BAC: góc lớn nhất từ vệ tinh có thể truyền tín hiệu đến Trái Đất.
Nghiên cứu độ lớn các bán kính quỹ đạo của các hành tinh trong hệ Mặt Trời, Bô-đơ đã tìm ra quy luật sau (chuỗi Bô-đơ)Chuỗi số này gồm số 0 đứng trước một cấp số nhân có số hạng đầu tiên là 3 và công bội là 2. Nếu cộng 4 cho mỗi số hạng của chuỗi, rồi đem kết q thu được chia cho 10 thì ta sẽ tìm được giá trị gần đúng của bán kính qu đạo các hành tinh, tính theo đơn vị thiên văn.Số hạng 0 ứng với quỹ đạo Thuỷ tinh. Số hạng 96 ứng với quỹ đạo Thổ tin Chuỗi này chỉ đúng đến trường hợp của Thổ tinh....
Đọc tiếp
Nghiên cứu độ lớn các bán kính quỹ đạo của các hành tinh trong hệ Mặt Trời, Bô-đơ đã tìm ra quy luật sau (chuỗi Bô-đơ)
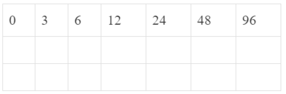
Chuỗi số này gồm số 0 đứng trước một cấp số nhân có số hạng đầu tiên là 3 và công bội là 2. Nếu cộng 4 cho mỗi số hạng của chuỗi, rồi đem kết q thu được chia cho 10 thì ta sẽ tìm được giá trị gần đúng của bán kính qu đạo các hành tinh, tính theo đơn vị thiên văn.
Số hạng 0 ứng với quỹ đạo Thuỷ tinh. Số hạng 96 ứng với quỹ đạo Thổ tin Chuỗi này chỉ đúng đến trường hợp của Thổ tinh.
Hãy thực hiện các phép tính và điền các giá trị của bán kính quỹ đạo cá hành tinh vào hàng thứ hai của bảng trên.
Hãy ghi tên các hành tinh có các quỹ đạo tương ứng vào hàng thứ ba.
xem bảng dưới đây
| 0 | 3 | 6 | 12 | 24 | 48 | 96 |
| 0,4 | 0,7 | 1 | 1,6 | 2,6 | 5,2 | 10 |
| Thủy tinh | Kim tinh | Trái Đất | Hỏa tinh | ? | Mộc tinh | Thổ tinh |
Đúng 0
Bình luận (0)
chứng minh rằng trong một hình bình hành ,khoảng cách từ một điểm trên đường chéo đến 2 cạnh kể (2 cạnh kề cùng đi qua một đỉnh của hình bình hành ), tỉ lệ nghịch với 2 cạnh ấy
Nghiên cứu độ lớn các bán kính quỹ đạo của các hành tinh trong hệ Mặt Trời, Bô-đơ đã tìm ra quy luật sau (chuỗi Bô-đơ)Chuỗi số này gồm số 0 đứng trước một cấp số nhân có số hạng đầu tiên là 3 và công bội là 2. Nếu cộng 4 cho mỗi số hạng của chuỗi, rồi đem kết q thu được chia cho 10 thì ta sẽ tìm được giá trị gần đúng của bán kính qu đạo các hành tinh, tính theo đơn vị thiên văn.Số hạng 0 ứng với quỹ đạo Thuỷ tinh. Số hạng 96 ứng với quỹ đạo Thổ tin Chuỗi này chỉ đúng đến trường hợp của Thổ tinh....
Đọc tiếp
Nghiên cứu độ lớn các bán kính quỹ đạo của các hành tinh trong hệ Mặt Trời, Bô-đơ đã tìm ra quy luật sau (chuỗi Bô-đơ)
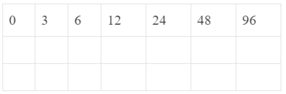
Chuỗi số này gồm số 0 đứng trước một cấp số nhân có số hạng đầu tiên là 3 và công bội là 2. Nếu cộng 4 cho mỗi số hạng của chuỗi, rồi đem kết q thu được chia cho 10 thì ta sẽ tìm được giá trị gần đúng của bán kính qu đạo các hành tinh, tính theo đơn vị thiên văn.
Số hạng 0 ứng với quỹ đạo Thuỷ tinh. Số hạng 96 ứng với quỹ đạo Thổ tin Chuỗi này chỉ đúng đến trường hợp của Thổ tinh.
Hãy thực hiện các phép tính và điền các giá trị của bán kính quỹ đạo cá hành tinh vào hàng thứ hai của bảng trên.
Hãy cho biết ý nghĩa của số hạng 24.
Số hạng ở cột 24 ứng với quỹ đạo của các tiểu hành tinh.
Đúng 0
Bình luận (0)
Chứng minh rằng khoảng cách từ một điểm nằm trên đường chéo của hình bình hành để các cạnh kề với đường chéo ấy thì tỉ lệ nghịch với các cạnh ấy.
DORAKID tự nhiên xông vào làm gì?
Đúng 0
Bình luận (0)
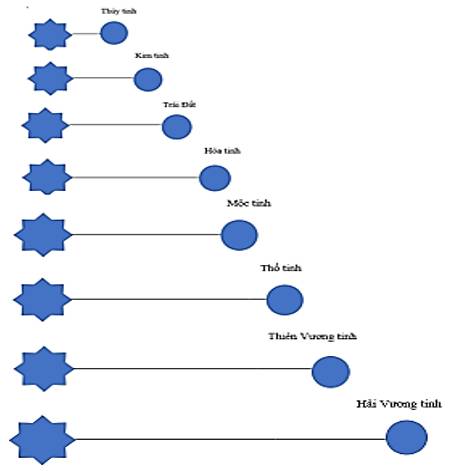
Vẽ sơ đồ biểu diễn khoảng cách từ Mặt Trời đến các hành tinh theo tỉ lệ 1cm ứng với 1 AU?
1.
Hành tinh | Thủy Tinh | Kim Tinh | Trái Đất | Hỏa Tinh | Mộc Tinh | Thổ Tinh | Thiên Vương Tinh | Hải Vương Tinh |
Khoảng cách (AU) | 0,39 | 0,72 | 1 | 1,52 | 5,2 | 9,54 | 19,2 | 30,07 |
Khoảng cách (cm) | 0,39cm | 0,72cm | 1cm | 1,52cm | 5,2cm | 9,54cm | 19,2cm | 30.07cm |
2.
Nhận xét: Các hành tinh ở càng xa Mặt Trời thì khoảng cách giữa các hành tinh càng lớn.
Đúng 0
Bình luận (0)
Trong nhiều thập kỷ, các chuyên gia đã cố gắng hiểu và giải thích lý do tại sao có rất nhiều cặp hành tinh nằm ngoài Hệ Mặt Trời của chúng ta có cấu hình bất thường như vậy.Những lần quan sát đã cho thấy nhiều hành tinh trong quỹ đạo bất thường dường như bị đẩy ra xa nhau, nhưng không biết lực nào gây ra như vậy.Nhưng giờ đây, các nhà thiên văn học cho rằng họ đã tìm ra câu trả lời. Họ thấy rằng có lực kỳ lạ cân bằng trên các cực hành tinh ngoại vi đã kéo chúng ra xa trọng tâm.Khám phá mới này g...
Đọc tiếp
Trong nhiều thập kỷ, các chuyên gia đã cố gắng hiểu và giải thích lý do tại sao có rất nhiều cặp hành tinh nằm ngoài Hệ Mặt Trời của chúng ta có cấu hình bất thường như vậy.
Những lần quan sát đã cho thấy nhiều hành tinh trong quỹ đạo bất thường dường như bị đẩy ra xa nhau, nhưng không biết lực nào gây ra như vậy.
Nhưng giờ đây, các nhà thiên văn học cho rằng họ đã tìm ra câu trả lời. Họ thấy rằng có lực kỳ lạ cân bằng trên các cực hành tinh ngoại vi đã kéo chúng ra xa trọng tâm.
Khám phá mới này giúp các nhà thiên văn học hiểu được cấu trúc, khí hậu và khả năng sinh sống của các hành tinh ngoại vi, trong khi chúng ta đang săn tìm hành tinh khác giống như Trái Đất.
Để hiểu những chi tiết kỳ lạ này, chúng ta trông chờ vào kính viễn vọng Kepler của NASA đang khám phá vũ trụ tìm các hành tinh ngoại vi. Kepler đã phát hiện ra rằng có đến 30% các ngôi sao giống với Mặt Trời, rồi đến các hành tinh được mệnh danh là Siêu Trái Đất.
Siêu Trái Đất thường lớn hơn Trái Đất, nhưng nhỏ hơn Sao Hải Vương. Thông thường, chúng quay quanh ngôi sao chủ của theo quỹ đạo tròn mất khoảng 100 ngày.
Thật thú vị, các nhà thiên văn học đã phát hiện ra rằng hầu hết các hành tinh này quay khoanh tròn thành từng cặp ngôi sao, với quỹ đạo kỳ lạ và không ổn định.
Sau khi thu thập đủ dữ liệu từ quan sát, các nhà khoa học tin rằng các tính năng kỳ quặc có thể được giải thích bằng hiện tượng được gọi là độ lệch xiên, nêu ra vì sao chúng bị nghiêng giữa trục và quỹ đạo.
Các nhà thiên văn học từ Đại học Yale (Mỹ) cho rằng một số các hành tinh này bị nghiêng đầu nên đẩy chúng ra xa nhau hơn.
Khi các hành tinh này có độ nghiêng dọc trục lớn, trái ngược với độ nghiêng nhỏ hoặc không nghiêng, thủy triều của chúng có tác dụng biến năng lượng quỹ đạo thành nhiệt trong các hành tinh. Lúc này, sự phân tán thủy triều mạnh mẽ ngăn cách các quỹ đạo.
Thật kỳ lạ, khi hiện tượng như vậy xảy ra trong Hệ Mặt Trời nếu chúng ta nhìn vào Trái Đất và Mặt trăng. Quỹ đạo Mặt Trăng dường như phát triển chậm, nhưng ngày trên Trái Đất đang kéo dài ra, khi Trái Đất và Mặt Trăng di chuyển xa hơn.
Thế nhưng, độ nghiêng kỳ lạ mang tính quyết định nhiều tính năng của các hành tinh. Nó tác động đến một số đặc điểm vật lý, như khí hậu, thời tiết và lưu thông toàn cầu.
Các mùa trên một hành tinh có độ nghiêng trục dọc khắc nghiệt hơn nhiều so với các mùa trên một hành tinh được sắp xếp hợp lý và các kiểu thời tiết của chúng có lẽ không quan trọng.
Theo khoahoc.tv Từ: Võ Lâm Anh
Đề bàiĐịnh luật thứ ba của Kepler về quỹ đạo chuyển động cho biết cách ước tính khoảng thời gian P (tính theo năm Trái Đất) mà một hành tinh cần để hoàn thành một quỹ đạo quay quanh Mặt Trời. Khoảng thời gian đó được xác định bởi hàm số P {d^{frac{3}{2}}}, trong đó d là khoảng cách từ hành tinh đó đến Mặt Trời tính theo đơn vị thiên văn AU (1 AU là khoảng cách từ Trái Đất đến Mặt Trời, tức là 1 AU khoảng 93 000 000 dặm). Hỏi Sao Hỏa quay quanh Mặt Trời thì mất bao nhiêu năm Trái Đất (làm tròn đ...
Đọc tiếp
Đề bài
Định luật thứ ba của Kepler về quỹ đạo chuyển động cho biết cách ước tính khoảng thời gian P (tính theo năm Trái Đất) mà một hành tinh cần để hoàn thành một quỹ đạo quay quanh Mặt Trời. Khoảng thời gian đó được xác định bởi hàm số \(P = {d^{\frac{3}{2}}}\), trong đó d là khoảng cách từ hành tinh đó đến Mặt Trời tính theo đơn vị thiên văn AU (1 AU là khoảng cách từ Trái Đất đến Mặt Trời, tức là 1 AU khoảng 93 000 000 dặm). Hỏi Sao Hỏa quay quanh Mặt Trời thì mất bao nhiêu năm Trái Đất (làm tròn đến kết quả hàng phần trăm)? Biết khoảng cách từ Sao Hỏa đến Mặt Trời là 1,52 AU.
Số năm Trái Đất để sao Hỏa quay quanh mặt trời là:
\(P=d^{\dfrac{3}{2}}=1.52^{1,5}\simeq1,87\left(AU\right)\)
Đúng 1
Bình luận (0)
Hỏa Tinh quay quanh Mặt Trời một vòng hết 687 ngày, ở khoảng cách 2,3.1011 m. Khối lượng của Hỏa Tinh là 6,4.1023 kg. Tính:
a) Tốc độ trên quỹ đạo của Hỏa Tinh.
b) Gia tốc hướng tâm của Hỏa Tinh.
c) Lực hấp dẫn mà Mặt Trời tác dụng lên Hỏa Tinh.
Ta có: 867 ngày = 867.86400 s; R = 2,3.1011 m; m = 6,4.1023 kg.
a) Tốc độ trên quỹ đạo của Hỏa Tính là: \(v = \omega .R = \frac{{2\pi }}{T}.R = \frac{{2\pi }}{{687.86400}}.2,{3.10^{11}} \approx 24346,54(m/s)\)
b) Gia tốc hướng tâm của Hỏa Tinh là:
\({a_{ht}} = \frac{{{v^2}}}{R} = \frac{{24346,{{54}^2}}}{{2,{{3.10}^{11}}}} \approx 5,{6.10^{ - 3}}(m/{s^2})\)
c) Lực hấp dẫn mà Mặt Trời tác dụng lên Hỏa Tinh chính là lực hướng tâm của Hỏa Tinh
=> \({F_{ht}} = m.{a_{ht}} = 6,{4.10^{23}}.2,{6.10^{ - 3}} = 16,{64.10^{20}}(N)\)
Vậy lực hấp dẫn mà Mặt Trời tác dụng Hỏa Tinh là 16,64.1020 N.
Đúng 0
Bình luận (0)
















