Giá trị của biểu thức sin 36 0 - cos 54 0 bằng:
A. 0
B. 2 sin 36 0
C. 2 cos 54 0
D. 1
Giá trị của biểu thức:
sin 36\(^0\)-cos54\(^0\)+cos60\(^0\)
sin \(^210^0\)+sin\(^230^0\)+sin\(^280^0\)+sin\(^260^0\)
a: \(\sin36^0-\cos54^0+\cos60^0\)
\(=\sin36^0-\sin36^0+\dfrac{1}{2}=\dfrac{1}{2}\)
b: \(=\left(\sin^210^0+\sin^280^0\right)+\left(\sin^230^0+\sin^260^0\right)\)
=1+1=2
`sin36^o -cos54^o +cos60^o`
`=cos54^o -cos54^o +cos60^o`
`=cos60^o=1/2`
_____________________________________________
`sin^2 10^o +sin^2 30^o +sin^2 80^o +sin^2 60^o`
`=cos^2 80^o +cos^2 60^o +sin^2 80^o +sin^2 60^o`
`=(cos^2 80^2 +sin^2 80^o )+(cos^2 60^o +sin^2 60^o )`
`=1+1=2`
Tính giá trị của biểu thức:
a) a sin 0 độ + b cos 0 độ + c sin 90 độ
b) a cos 90 độ + b sin 90 độ + c sin 180 độ
c) \(a^2sin90\) độ + b bình cos 90 độ + c bình cos 180 độ
a:\(a\cdot sin0+b\cdot cos0+c\cdot sin90\)
\(=a\cdot0+b\cdot1+c\cdot1\)
=b+c
b: \(a\cdot cos90+b\cdot sin90+c\cdot sin180\)
\(=a\cdot0+b\cdot1+c\cdot0\)
=b
c: \(a^2\cdot sin90+b^2\cdot cos90+c^2\cdot cos180\)
\(=a^2\cdot1+b^2\cdot0+c^2\left(-1\right)\)
\(=a^2-c^2\)
Tính giá trị của biểu thức:
\(A=\frac{3\cos67^0}{2\tan23^0}-\frac{\cos^236^0+\cos^254^0-\cos^217^0-\cos^273^0}{\sin^224^0+\sin^266^0+\sin^215^0+\sin^275^0}\)
Tính giá trị của biểu thức:
a,A= \(sin^215^0+sin^240^0+sin^260^0+sin^275^0+sin^250^0+sin^230^0\)
b, B=\(tan5^0tan10^0....tan85^0\)
c, C=\(cos^215^0-cos^225^0+cos^235^0-cos^245^0-cos^265^0+cos^275^0\)
LÀM ƠN GIÚP MÌNH NHÉ, MAI NỘP RÙI. PLEASE!!!!!!
Có
A=\(\left(sin^215^o+sin^275^o\right)+\left(sin^240^o+sin^250^o\right)+\left(sin^260^o+sin^230^o\right)\)
\(=\left(sin^215^o+cos^215^o\right)+...\)
\(=1\cdot3=3\)
Câu c tương tự mà mk nghĩ đề sai dấu - trước cos^245độ
Nói chung nếu: a+b=90 độ
thì: \(sin^2a+sin^2b=1\)
b) thì áp dụng nếu a+b=90 độ:
\(tana=cotb\) và ngược lại
Mà \(tana\cdot cota=1\)
Nói chung là công thức......
Tính giá trị của biểu thức
A=\(\sin^210^0+\sin^220^0+\sin^230^0+...+\sin^280^0+2013\)
B=\(\cos^21^0+\cos^22^0+...+\cos^289^0\)
C=\(\frac{\sin33^0}{\cos57^0}+\frac{\tan32^0}{\cot58^0}-2\left(\sin20^0.\cos70^0+\cos20^0.\sin70^0\right)\)
D=\(4\cos^2a-6\sin^2a\) biết \(\sin a=\frac{1}{5}\)
Tính giá trị đúng của các biểu thức sau (không dùng máy tính cầm tay):
a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
b) \(B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}\)
c) \(C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
a) \(A = \cos {0^o} + \cos {40^o} + \cos {120^o} + \cos {140^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\cos {0^o} = 1;\;\cos {120^o} = - \frac{1}{2}\)
Lại có: \(\cos {140^o} = - \cos \left( {{{180}^o} - {{40}^o}} \right) = - \cos {40^o}\)
\(\begin{array}{l} \Rightarrow A = 1 + \cos {40^o} + \left( { - \frac{1}{2}} \right) - \cos {40^o}\\ \Leftrightarrow A = \frac{1}{2}.\end{array}\)
b) \(B = \sin {5^o} + \sin {150^o} - \sin {175^o} + \sin {180^o}\)
Tra bảng giá trị lượng giác của một số góc đặc biệt, ta có:
\(\sin {150^o} = \frac{1}{2};\;\sin {180^o} = 0\)
Lại có: \(\sin {175^o} = \sin \left( {{{180}^o} - {{175}^o}} \right) = \sin {5^o}\)
\(\begin{array}{l} \Rightarrow B = \sin {5^o} + \frac{1}{2} - \sin {5^o} + 0\\ \Leftrightarrow B = \frac{1}{2}.\end{array}\)
c) \(C = \cos {15^o} + \cos {35^o} - \sin {75^o} - \sin {55^o}\)
Ta có: \(\sin {75^o} = \cos\left( {{{90}^o} - {{75}^o}} \right) = \cos {15^o}\); \(\sin {55^o} = \cos\left( {{{90}^o} - {{55}^o}} \right) = \cos {35^o}\)
\(\begin{array}{l} \Rightarrow C = \cos {15^o} + \cos {35^o} - \cos {15^o} - \cos {35^o}\\ \Leftrightarrow C = 0.\end{array}\)
d) \(D = \tan {25^o}.\tan {45^o}.\tan {115^o}\)
Ta có: \(\tan {115^o} = - \tan \left( {{{180}^o} - {{115}^o}} \right) = - \tan {65^o}\)
Mà: \(\tan {65^o} = \cot \left( {{{90}^o} - {{65}^o}} \right) = \cot {25^o}\)
\(\begin{array}{l} \Rightarrow D = \tan {25^o}.\tan {45^o}.(-\cot {25^o})\\ \Leftrightarrow D =- \tan {45^o} = -1\end{array}\)
e) \(E = \cot {10^o}.\cot {30^o}.\cot {100^o}\)
Ta có: \(\cot {100^o} = - \cot \left( {{{180}^o} - {{100}^o}} \right) = - \cot {80^o}\)
Mà: \(\cot {80^o} = \tan \left( {{{90}^o} - {{80}^o}} \right) = \tan {10^o}\Rightarrow \cot {100^o} =- \tan {10^o}\)
\(\begin{array}{l} \Rightarrow E = \cot {10^o}.\cot {30^o}.(-\tan {10^o})\\ \Leftrightarrow E = -\cot {30^o} =- \sqrt 3 .\end{array}\)
Cho sin a = 3/5 và cos a < 0 ; cos b = 3/4 và sin b > 0. Giá trị của sin(a - b) bằng :
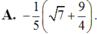
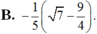
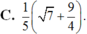
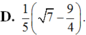
Chọn C.
Ta có :
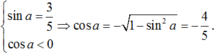
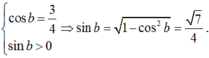
Áp dụng công thức cộng ta có:
sin(a – b) = sin a.cos b – cos a.sin b
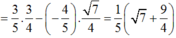
Tính giá trị các biểu thức sau:
a) A = cos2520 sin450 + sin2520cos450
b) B = sin450cos2470 + sin2470cos450
Chú ý 2 điều: \(\cos45^o=\sin45^o=\frac{\sqrt{2}}{2}\) và \(\cos^2a+\sin^2a=1\)
Do đó:
a) \(A=\cos^252^o.\frac{\sqrt{2}}{2}+\sin^252^o.\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{2}\left(\cos^252^o+\sin^252^o\right)=\frac{\sqrt{2}}{2}.1=\frac{\sqrt{2}}{2}\)
b) \(B=\frac{\sqrt{2}}{2}.\cos^247^o+\frac{\sqrt{2}}{2}.\sin^247^o=\frac{\sqrt{2}}{2}\left(\cos^247^o+\sin^247^o\right)=\frac{\sqrt{2}}{2}.1=\frac{\sqrt{2}}{2}\)
tìm giá trị lớn nhất và giá trị nhỏ nhất của các biểu thức sau :
a) \(a\sin x+b\cos x\) ( a và b là các hằng số , \(a^2+b^2\) khác 0 )
b) \(\sin^2x+\sin x\cos x+3\cos^2x\)
c) \(A\sin^2x+B\sin x\cos x+C\cos^2x\) (A , B , C là các hằng số )
heo me tim gtnn gtln cua bieu thuc:asinx + bcosx (a,b la hang so,a^2+b^2=/o)? | Yahoo Hỏi & Đáp
Tính giá trị biểu thức:
a) \(\sin^230^0-\sin^240^0-\sin^250^0+\sin^260^0\)
b) \(\cos^225^0-\cos^235^0+\cos^245^0-\cos^255^0+\cos^265^0\)
Vì sin(\(\alpha\) ) = cos (\(90-\alpha\)) nên \(sin^2\alpha=cos^2\left(90-\alpha\right)\)
a/ \(sin^230-sin^240-sin^250+sin^260=\left(cos^260+sin^260\right)-\left(cos^250+sin^250\right)=1-1=0\)
b/ \(cos^225-cos^235+cos^245-cos^255+cos^265=\left(sin^265+cos^265\right)-\left(sin^255+cos^255\right)+cos^245=1-1+cos^245=cos^245=\dfrac{1}{2}\)