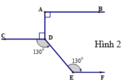
Trong hình 2, có A B ⊥ A D , C D ⊥ A D , C D E ^ = 130 0 và D E F ^ = 130 0 . Chứng minh EF // AB
Các hình dưới đây không được vẽ theo tỷ lệ. Hình nào trong 2 hình có độ dài bằng nhau? *
Trong Hình 94, hình chữ nhật ABCD có AB = 9 cm, AD = 6 cm; hình chữ nhật A’B’C’D’ có A’B’ = 3 cm, A’D’ = 2 cm; hình chữ nhật A’’B’’C’’D’’ có A’’B’’ = 3 cm, A’’D’’ = 2 cm. Quan sát Hình 94 và cho biết:
a) Hai hình chữ nhật A’’B’’C’’D’’, ABCD có đồng dạng phối cảnh hay không.
b) Hai hình chữ nhật A’B’C’D’, A’’B’’C’’D’’ có bằng nhau hay không.
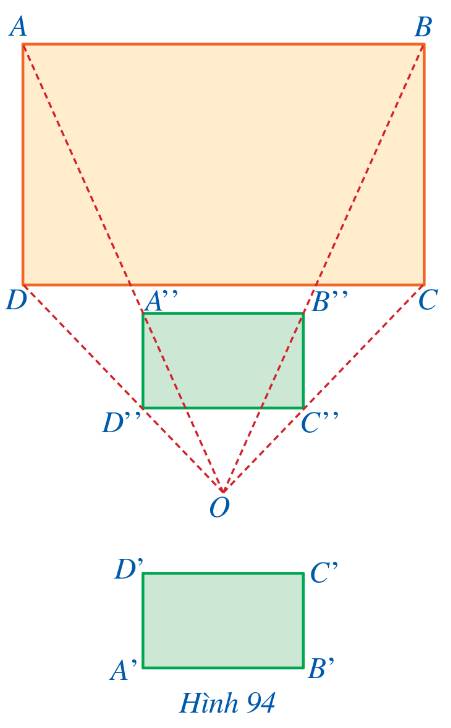
a: Xét ΔODC có D''C''//DC
nên \(\dfrac{D''C''}{DC}=\dfrac{OD''}{OD}=\dfrac{OC''}{OC}=\dfrac{3}{9}=\dfrac{1}{3}\)(1)
Xét ΔOAB có A''B"//AB
nên \(\dfrac{A"B"}{AB}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}=\dfrac{3}{9}=\dfrac{1}{3}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{OD"}{OD}=\dfrac{OC"}{OC}=\dfrac{OA"}{OA}=\dfrac{OB"}{OB}\)
mà A"A, B"B, C"C, D"D đều đi qua điểm O
nên hai hình hộp chữ nhật A"B"C"D" và ABCD đồng dạng phối cảnh với nhau
b: ta có: A'B'=C'D'=3cm
A"B"=C"D"=3cm
Do đó: A"B"=C"D"=A'B'=C'D'(3)
ta có: A'D'=B'C'=2cm
A"D"=B"C"=2cm
Do đó: A'D'=B'C'=A"D"=B"C"(4)
Từ (3),(4) suy ra hai hình hộp chữ nhật A"B"C"D" và A'B'C'D' bằng nhau
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)
CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)
CH 3. Trong không gian Oxyz cho 2 vectơ a =(1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8
CH 4.Trong không gian Oxyz cho 2 vecto a= (3; 1; 2) và b= (2; 0; -1); khi đó vectơ 2a-b có độ dài bằng : А. 3/5 В. 29 С. M D. S/5
CH 5. Cho hình bình hành ABCD với A (-1;0;2), B(3;4;0) D (5;2;6). Tìm khẳng định sai. A. Tâm của hình bình hành có tọa độ là (4;3;3) B. Vecto AB có tọa độ là (4;-4;-2) C. Tọa độ của điểm C là (9;6;4) D. Trọng tâm tam giác ABD có tọa độ là (3;2;2)
Cặp lực nào trong hình 5.3 là cặp lực cân bằng?
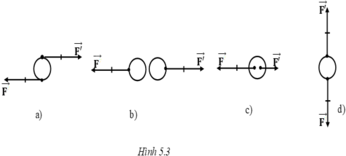
A. Trong hình a.
B. Trong hình a và b.
C. Trong hình c và d.
D. Trong hình d.
Chọn D.
Vì cặp lực cân bằng là cặp lực cùng đặt lên một vật có cường độ bằng nhau, phương nằm trên cùng một đường thẳng và ngược chiều nhau.
1.Chu vi của hình tròn có đường kính 6dm là:....................dm
2.Trong hình bên,AH là đường cao của mấy hình tam giác ?.
A.3 hình
B.4 hình
C.5 hình
D.6 hình
Câu 1 : 18, 84 dm
Câu 2 ( ko có hình )
Câu 1: `P=6×3,14=18,84(dm)`
2.Trong hình bên,AH là đường cao của mấy hình tam giác ?.
A.3 hình
B.4 hình
C.5 hình
D.6 hình
1.cho tỉ lệ thức: a+b+c/a+b-c=a-b+c/a-b-c trong đó b khác 0. cmr:c=0
2.cmr ta có tỉ lệ thức a/b=c/d nếu có một trong các đẳng thức sau:
(a+b+c+d)(a-b-c+d)=(a-b+c-d)(a+b-c-d)
GIÚP MÌNH ĐI CÁC BẠN ƠI!
Chọn kết quả đúng trong các kết quả dưới đây:
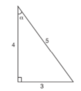
a) Trong hình 41, sin α bằng:
( A ) 5 3 ( B ) 5 4 ( C ) 3 5 ( D ) 3 4
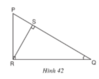
b) Trong hình 42, sin Q bằng:
( A ) PR RS ( B ) PR QR ( C ) PS SR ( D ) SR QR
c) Trong hình 43, cos 30o bằng:
( A ) 2 a 3 ( B ) a 3 ( C ) 3 2 ( D ) 2 3 a 2

Cho a, b, c, d là các số thực thỏa mãn a < b < c < d và các mệnh đề sau:
(I) ( a ; b ) ∩ ( c ; d ) = ∅
(II) ( a ; c ] ∩ [ b ; d ) = ( b ; c )
(III) ( a ; c ] ∪ ( b ; d ] = ( a ; d ]
(IV) ( − ∞ ; b ) \ ( a ; d ) = ( − ∞ ; a ]
(V) ( b ; d ) \ ( a ; c ) = ( c ; d )
(VI) ( a ; d ) \ ( b ; c ) = ( a ; b ] ∪ [ c ; d )
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 5
B. 4
C. 3
D. 2
Các mệnh đề đúng là (I), (III), (IV), (VI).
Đáp án B
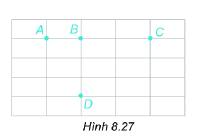
Với bốn điểm A, B, C, D như hình 8.27, em hãy kể tên các đoạn thẳng có đầu mút là:
a) Hai trong ba điểm A, B, C;
b) Hai trong bốn điểm A, B, C, D.
a. Các đoạn thẳng là : AB, AC, BC.
b. Các đoạn thẳng là: AB, AC, AD, BC, BD, CD.
CMR:ta có tỉ lệ thức a/b=c/d nếu có 1 trong các đẳng thức sau:
(a+b+c+d)(a-b-c+d)=(a-b+c-d)(a+b-c-d)
(a+b+c+d)(a-b-c+d)=(a-b+c-d)(a+b-c-d) => \(\frac{a+b+c+d}{a+b-\left(c+d\right)}=\frac{a-b+c-d}{a-b-\left(c-d\right)}\)
Áp dụng t/c của dãy tỉ số bằng nhau ta có:
\(\frac{a+b+c+d}{a+b-\left(c+d\right)}=\frac{a-b+c-d}{a-b-\left(c-d\right)}=\frac{\left(a+b+c+d\right)+\left(a-b+c-d\right)}{\left(a+b-\left(c+d\right)\right)+\left(a-b-\left(c-d\right)\right)}=\frac{\left(a+b+c+d\right)-\left(a-b+c-d\right)}{\left(a+b-\left(c+d\right)\right)-\left(a-b-\left(c-d\right)\right)}\)
=> \(\frac{a+c}{a-c}=\frac{b+d}{b-d}\)=> \(\frac{a+c}{b+d}=\frac{a-c}{b-d}\) => \(\frac{\left(a+c\right)+\left(a-c\right)}{\left(b+d\right)+\left(b-d\right)}=\frac{\left(a+c\right)-\left(a-c\right)}{\left(b+d\right)-\left(b-d\right)}\)=> \(\frac{a}{b}=\frac{c}{d}\)
Vậy...