Giải phương trình tanx + tan2x = -sin3x.cos2x.
A. x = k π 3 ; x = π + k2π
B. x = k π 3 ; x = π 2 + k2π
C. x = k π 3
D. x = k2π
Bài4: Giải phương trình a/ cos2x - sin7x = 0. b/ tan( 15° - x ) = cot x c/ tanx X tan2x = 1
a, cos2x - sin7x = 0
⇔ cos2x = sin7x
⇔ cos2x = cos \(\left(7x-\dfrac{\pi}{2}\right)\)
⇔ \(\left[{}\begin{matrix}7x-\dfrac{\pi}{2}=2x+k2\pi\\7x-\dfrac{\pi}{2}=-2x+k2\pi\end{matrix}\right.\) với k là số nguyên
⇔ \(\left[{}\begin{matrix}x=\dfrac{\pi}{10}+\dfrac{k.2\pi}{5}\\x=\dfrac{\pi}{18}+\dfrac{k2\pi}{9}\end{matrix}\right.\) với k là số nguyên
Tìm GTLN GTNN
y = 2cos22x + 2cos2x - 4
y = tan2x - 2√3 tanx -1 ∀ x ∈ [ -π/4 ; π/3 ]
a.
Đặt \(cos2x=t\Rightarrow t\in\left[-1;1\right]\)
Xét hàm \(y=f\left(t\right)=2t^2+2t-4\) trên \(\left[-1;1\right]\)
\(-\dfrac{b}{2a}=-\dfrac{1}{2}\in\left[-1;1\right]\)
\(f\left(-1\right)=-4\) ; \(f\left(-\dfrac{1}{2}\right)=-\dfrac{9}{2}\) ; \(f\left(1\right)=0\)
\(\Rightarrow y_{min}=-\dfrac{9}{2}\) khi \(t=-\dfrac{1}{2}\) hay \(cos2x=-\dfrac{1}{2}\)
\(y_{max}=0\) khi \(cos2x=1\)
b. Đặt \(tanx=t\Rightarrow t\in\left[-1;\sqrt{3}\right]\)
Xét hàm \(f\left(t\right)=t^2-2\sqrt{3}t-1\) trên \(\left[-1;\sqrt{3}\right]\)
\(-\dfrac{b}{2a}=\sqrt{3}\in\left[-1;\sqrt{3}\right]\)
\(f\left(-1\right)=2\sqrt{3}\) ; \(f\left(\sqrt{3}\right)=-4\)
\(y_{min}=-4\) khi \(x=\dfrac{\pi}{3}\) ; \(y_{max}=2\sqrt{3}\) khi \(x=-\dfrac{\pi}{4}\)
Giải phương trình: Tan(x-π/4) = Tan2x
\(\Leftrightarrow2x=x-\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\) (\(k\in Z\))
Giải phương trình: tanx + tan2x - tan3x = 0
Giải theo công thức tan(x+2x)=(tanx+tan2x)/(1-tanx.tan2x) có vẻ nhanh hơn đó.
Nhưng nhớ phải đặt điều kiện cho 3 cái cos dưới mẫu khác 0 (đk riêng của pt lượng giác)
Giải phương trình : sin5x-sin3x=0
Giải phương trình sau: tanx + tan (x+π/4) = 1
Điều kiện:
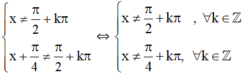
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
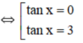
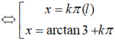
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }
giải phương trình
a) \(tanx=1\)
b) \(tanx=tan55\) độ
c) \(tan2x=tan\dfrac{\pi}{5}\)
d) \(tan\left(2x+\dfrac{\pi}{3}\right)\)= 0
e) \(cot\left(x-\dfrac{\pi}{3}\right)=0\)
Để giải các phương trình này, chúng ta cần sử dụng các quy tắc và công thức của hàm lượng giác. Hãy xem xét từng phương trình một cách cụ thể:
a) Để giải phương trình tan(x) = 1, chúng ta có thể sử dụng công thức x = arctan(1) để tìm giá trị của x.
b) Để giải phương trình tan(x) = tan(55°), chúng ta có thể sử dụng công thức x = arctan(tan(55°)) để tìm giá trị của x.
c) Để giải phương trình tan(2x) = tan(π/5), chúng ta có thể sử dụng công thức 2x = arctan(tan(π/5)) để tìm giá trị của 2x, sau đó chia kết quả cho 2 để tìm giá trị của x.
d) Để giải phương trình tan(2x+π/3) = 0, chúng ta có thể sử dụng công thức 2x+π/3 = arctan(0) để tìm giá trị của 2x+π/3, sau đó giải phương trình để tìm giá trị của x.
e) Để giải phương trình cot(x-π/3) = 0, chúng ta có thể sử dụng công thức x-π/3 = arccot(0) để tìm giá trị của x-π/3, sau đó giải phương trình để tìm giá trị của x.
Hy vọng những thông tin này sẽ giúp bạn giải quyết các phương trình trên. Nếu bạn cần thêm thông tin hoặc giải thích chi tiết hơn, xin vui lòng cho biết.
a: tan x=1
=>tan x=tan(pi/4)
=>x=pi/4+kpi
b: tan x=tan 55 độ
=>x=55 độ+k*180 độ
c: tan 2x=tan pi/5
=>2x=pi/5+kpi
=>x=pi/10+kpi/2
d: tan(2x+pi/3)=0
=>2x+pi/3=kpi
=>2x=-pi/3+kpi
=>x=-pi/6+kpi/2
e: cot(x-pi/3)=0
=>x-pi/3=pi/2+kpi
=>x=5/6pi+kpi
Họ nghiệm của phương trình tan(x+\(\frac{\pi}{5}\))+ \(\sqrt{3}\)= 0 là?
Phương trình tanx= tanx/2 có họ nghiệm là?
Nghiệm của phương trình √3 + 3tanx =0 có nghiệm là?
Phương trình √3 + tanx = 0 có nghiệm là?
Họ nghiệm của phương trình tan2x - tanx = 0 là?
Phương trình lượng giác 3cotx - √3 = 0 có nghiệm là?
Pt lượng giác 2cotx - √3 = 0 có nghiệm là?
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x − sin x = 3 tan x là.
A. 0
B. 1.
C. 2
D. 3
Đáp án B
TABLE f ( x ) = tan x + sin x + tan x − sin x − 3 tan x đổi dấu 1 lần trong 0 ; π ⇒ 1 nghiệm
Số nghiệm thuộc khoảng 0 ; π của phương trình tan x + sin x + tan x - sin x = 3 tan x là
A. 0.
B. 1.
C. 2.
D. 3.