Giải phương trình: cos5x + x2 0 A. B. C. D.Vô nghiệm
Đọc tiếp
Giải phương trình: cos5x + x2 = 0
A. 
B. 
C. 
D.Vô nghiệm
Những câu hỏi liên quan
13 tháng 2 2023 lúc 21:30
Có bao nhiêu giá trị của tham số m để hai phương trình x2+mx+1=0 và x2+x+m=0 có nghiệm chung
A.0 B.1 C.2 D.Vô số
1. Cho phương trình x2 -2mx-4m-5=0 (x là ẩn số, m là tham số). a) Chứng minh rằng phương trình luôn luôn có nghiệm với mọi m. b) Gọi x1, x2 là các nghiệm của phương trình. Tìm m để biểu thức A = đạt giá trị nhỏ nhất.
\(a,\Delta'=\left(-m\right)^2-\left(4m-5\right)=m^2-4m+5=\left(m^2-4m+4\right)+1=\left(m-2\right)^2+1>0\)
Vậy pt luôn có 2 nghiệm phân biệt với mọi m
câu b thiếu
Đúng 1
Bình luận (0)
Có bao nhiêu giá trị thực của tham số m để bất phương trình (m2-4)x<m+2 vô nghiệm
A.0 B.1 C.2 D.vô số
(cho mình lời giải chi tiết nha)
BPT đã cho vô nghiệm khi:
\(\left\{{}\begin{matrix}m^2-4=0\\m+2\le0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=\pm2\\m\le-2\end{matrix}\right.\) \(\Rightarrow m=-2\)
B đúng
Đúng 0
Bình luận (0)
Giải phương trình sau: sin3x - cos5x = 0
sin3x - cos5x = 0
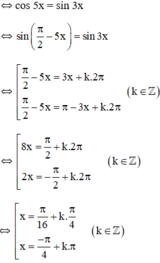
Vậy phương trình có hai họ nghiệm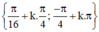 
(k ∈ Z).
Đúng 0
Bình luận (0)
Giải các phương trình:
\(a,sinx-cosx=1\)
\(b,cos3x.cos2x=cos5x\)
a, \(sinx-cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
Đúng 2
Bình luận (0)
b, \(cos3x.cos2x=cos5x\)
\(\Leftrightarrow\dfrac{1}{2}cos5x+\dfrac{1}{2}cosx=cos5x\)
\(\Leftrightarrow cosx=cos5x\)
\(\Leftrightarrow5x=\pm x+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\dfrac{k\pi}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho phương trình x2 +( m-1)x - m 0 (5)a/ Chứng tỏ rằng phương trình (5) luôn có nghiệm với mọi giá trị của m ?b/ Gọi x1 và x2 là nghiệm của phương trình (5) Chứng minh hệ thức x1^2 +x2^2 -2.x1.x2 -x1^2.x2^2 2m+1
Đọc tiếp
Cho phương trình x2 +( m-1)x - m = 0 (5)
a/ Chứng tỏ rằng phương trình (5) luôn có nghiệm với mọi giá trị của m ?
b/ Gọi x1 và x2 là nghiệm của phương trình (5) Chứng minh hệ thức
x1^2 +x2^2 -2.x1.x2 -x1^2.x2^2 =2m+1
a: \(\text{Δ}=\left(m-1\right)^2-4\cdot1\cdot\left(-m\right)=\left(m+1\right)^2>=0\)
=>(5) luôn có nghiệm
b: \(x_1^2+x_2^2-2x_1x_2-\left(x_1\cdot x_2\right)^2=2m+1\)
=>\(\left(x_1+x_2\right)^2-4x_1x_2-\left(x_1\cdot x_2\right)^2=2m+1\)
=>\(\left(m-1\right)^2-4\cdot\left(-m\right)-\left(-m\right)^2=2m+1\)
=>\(m^2-2m+1+4m-m^2=2m+1\)
=>2m+1=2m+1(luôn đúng)
Đúng 0
Bình luận (0)
Câu 1: Phương trình lượng giác: sin^2 x - 3cos x - 4 = 0 có nghiệm là: A. x=- pi 2 +k 2 pi B. x=- pi+k2 pi C. x = pi/6 + k*pi D.Vô nghiệm
1.D
sin2x - 3cosx - 4 = 0
1-cos2x - 3cosx - 4 = 0
cos2x + 3 cosx + 3 = 0
Vô nghiệm
Đúng 0
Bình luận (0)
Giải các phương trình sau :
a) \(\sin3x-\cos5x=0\)
b) \(\tan3x.\tan x=1\)
Bài 7. a) sin 3x - cos 5x = 0 ⇔ cos 5x = sin 3x ⇔ cos 5x = cos (
- 3x) ⇔
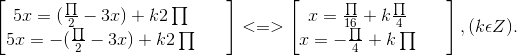
b) tan 3x . tan x = 1 ⇔ 
. Điều kiện : cos 3x . cos x # 0.
Với điều kiện này phương trình tương đương với
cos 3x . cos x = sin 3x . sinx ⇔ cos 3x . cos x - sin 3x . sinx = 0 ⇔ cos 4x = 0.
Do đó
tan 3x . tan x = 1 ⇔ 
⇔ cos 2x = 
⇔ cos 4x = 0
⇔ 
Đúng 0
Bình luận (0)
Help me! (Lớp 11)
giải phương trình sau:
sin3x - cos5x = 0
\(\sin3x-\cos5x=0\Leftrightarrow\cos5x=\sin3x\Leftrightarrow\cos5x=\cos\left(\frac{\pi}{2}-3x\right)\)
\(\Leftrightarrow5x=\pm\left(\frac{\pi}{2}-3x\right)+k2\pi\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{16}+k\frac{\pi}{4}\\x=-\frac{\pi}{4}+k\pi,k\in Z\end{cases}}\)
Đúng 0
Bình luận (0)