Biểu thức 5 - 2 x xác định khi:
A. x > 5 2
B. x ≤ 5 2
C. x ≥ 5 2
D. x < 5 2
Cho biểu thức
2
2 5 1
25 5 5
x
A
x x x
= − −
− − +
1) Tìm điều kiện xác định của biểu thức A.
2) Rút gọn biểu thức A.
3) Tính giá trị của biểu thức A khi
x =1.
đkxđ:\(x\ne5,x\ne-5\)
\(\dfrac{2x}{\left(x-5\right)\left(x+5\right)}-\dfrac{5}{x-5}-\dfrac{1}{x+5}\)
\(\dfrac{2x}{\left(x-5\right)\left(x+5\right)}-\dfrac{5x+25}{\left(x-5\right)\left(x+5\right)}-\dfrac{x-5}{\left(x-5\right)\left(x+5\right)}\)
\(\dfrac{2x-5x-25-x+5}{\left(x-5\right)\left(x+5\right)}=\dfrac{-4x-20}{\left(x-5\right)\left(x+5\right)}=\dfrac{-4\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}=-\dfrac{4}{x-5}\)
thay x=1 vào bt A, ta được:
\(-\dfrac{4}{1-5}=1\)
cho biểu thức B=[ x+1/ 2x-2 +3/x2 -1 -x+3/2x+2] .2x2 -2/5
a, tìm điều kiện của biến để phân thức xác định
b, c/m rằng khi giá trị của biểu thức xác định thì nó không phụ thuộc vào biến x ?
Cho các biểu thức A= \(\dfrac{X+2}{X+3}-\dfrac{5}{X^2+X-6}+\dfrac{1}{2-X}\)
a) Tìm điều kiện xác định của A
b) Rút gọn biểu thức A.
c) Tính giá trị của biểu thức A khi x = 3
a) ĐKXĐ: \(x\ne-3,x\ne2\)
b) \(A=\dfrac{\left(x-2\right)\left(x+2\right)-5-\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}=\dfrac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}=\dfrac{\left(x+3\right)\left(x-4\right)}{\left(x+3\right)\left(x-2\right)}=\dfrac{x-4}{x-2}\)
c) \(A=\dfrac{x-4}{x-2}=\dfrac{3-4}{3-2}=-1\)
Bài 1: Ph tích thành nhân tử
b) x^5-x^3-x^2+1
Bài 2: Cho biểu thức 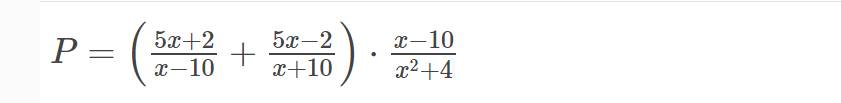
a) tìm điều kiện xác định của P
b) Rút gọn biểu thức P
c) tính giá trị của P khi x=2/5
Bài 2
a) ĐKXĐ: x - 10 0 và x + 10 0
*) x - 10 0
x 10
*) x + 10 0
x 10
Vậy ĐKXĐ: x -10; x 10
b) P = [(5x + 2)(x + 10) + (5x - 2)(x - 10)]/[(x - 10)(x + 10)] . (x - 10)/(x² + 4)
= (5x² + 50x + 2x + 20 + 5x² - 50x - 2x + 20)/[(x + 10)(x² + 4)]
= (10x² + 40)/[(x + 10)(x² + 4)]
= 10(x² + 4)/[(x + 10)(x² + 4)]
= 10/(x + 10)
c) Khi x = 2/5 ta có:
P = 10.(2/5 + 10)
= 4 + 100
= 104
Bài 1
b) x⁵ - x³ - x² + 1
= (x⁵ - x³) - (x² - 1)
= x³.(x² - 1) - (x² - 1)
= (x² - 1)(x³ - 1)
= (x - 1)(x + 1)(x - 1)(x² + x + 1)
= (x + 1)(x - 1)²(x² + x + 1)
Cho biểu thức: A=2x+20/x^2-25+1/x+5+2/x-5
a. Tìm điều kiện xác định của A.
b. Rút gọn biểu thức A.
c. Tính giá trị của biểu thức A khi x = 9.
d. Tìm x để A= –3
Cho biểu thức M= ( \(\dfrac{x}{x^2-25}\) \(-\)\(\dfrac{x-5}{x^2+5\alpha}\)) : \(\dfrac{2x-5}{x^2+5x}\)
a Tìm điều kiện xác định của biểu thức M được xác nhận
b rút gọn biểu thức M
a: ĐKXĐ: x<>0; x<>5; x<>5/2; x<>-5
b: \(M=\left(\dfrac{x}{\left(x-5\right)\left(x+5\right)}-\dfrac{x-5}{x\left(x+5\right)}\right):\dfrac{2x-5}{x\left(x+5\right)}\)
\(=\dfrac{x^2-x^2+10x-25}{x\left(x-5\right)\left(x+5\right)}\cdot\dfrac{x\left(x+5\right)}{2x-5}=\dfrac{1}{x-5}\)
Bài 2: Cho biểu thức 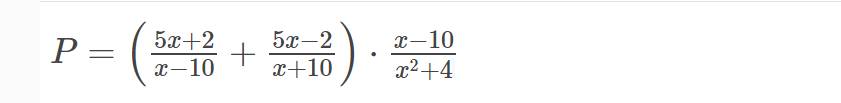
a) tìm điều kiện xác định của P
b) Rút gọn biểu thức P
c) Tính giá trị của P khi x=2/5
a) ĐKXĐ: \(x\ne\pm10\)
b) \(P=\left(\dfrac{5x+2}{x-10}+\dfrac{5x-2}{x+10}\right)\cdot\dfrac{x-10}{x^2+4}\left(x\ne\pm10\right)\)
\(=\left[\dfrac{\left(5x+2\right)\left(x+10\right)}{\left(x-10\right)\left(x+10\right)}+\dfrac{\left(5x-2\right)\left(x-10\right)}{\left(x-10\right)\left(x+10\right)}\right]\cdot\dfrac{x-10}{x^2+4}\)
\(=\dfrac{5x^2+52x+20+5x^2-52x+20}{\left(x-10\right)\left(x+10\right)}\cdot\dfrac{x-10}{x^2+4}\)
\(=\dfrac{10x^2+40}{x+10}\cdot\dfrac{1}{x^2+4}\)
\(=\dfrac{10\left(x^2+4\right)}{\left(x+10\right)\left(x^2+4\right)}\)
\(=\dfrac{10}{x+10}\)
c) Thay \(x=\dfrac{2}{5}\) vào \(P\), ta được:
\(P=\dfrac{10}{\dfrac{2}{5}+10}=\dfrac{25}{26}\)
\(\text{#}Toru\)
Cho biểu thức:
B = (\(\dfrac{x+1}{2x-2}\) + \(\dfrac{3}{x^2-1}\) - \(\dfrac{x+3}{2x+2}\)) . \(\dfrac{4x^2-4}{5}\)
a) Tìm điều kiện của x để giá trị của biểu thức được xác định.
b) C/m rằng: khi giá trị của x để giá trị của biểu thức được xác định.
cho biểu thức: \(\left[\frac{x+1}{2x-2}+\frac{3}{x^2-1}-\frac{x+3}{2x+2}\right].\frac{4x^2-4}{5}\)
a) tìm điều kiện của x để giá trị của biểu thức được xác định?
b) CMR: khi giá trị của biểu thức được xác định thì nó ko phụ thuộc vào giá trị của biến x
a) ĐKXĐ: \(\hept{\begin{cases}2x-2\ne0\\x^2-1\ne0\\2x+2\ne0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\ne1\\x\ne-1\end{cases}}\)
b) bạn rút gọn, biểu thức sẽ bằng 4
=> giá tri của biểu thức sẽ không phụ thuộc vào biến x
tôi vướng ở câu b giải cứ bị lẫn giải ra vẫn có biến x giải họ tôi cái
cho biểu thức:B=[(x+1/2x−2) +(3/x^2−1) −(x+3/2x+2)] .(4x^2−4/5 )
a, tìm điều kiện của x để giá trị của biểu thức được xác định?
b, CMR: khi giá trị của biểu thức được xác định thì nó không phụ thuộc vào giá trị của biến x
a) ĐK : \(x\ne1\); \(x\ne-1\)
b) Ta có biểu thức:
\(B=\left(\frac{x+1}{2x-2}+\frac{3}{x^2-1}-\frac{x+3}{2x+2}\right).\left(\frac{4x^2-4}{5}\right)\)
\(=\left(\frac{x+1}{2.\left(x-1\right)}+\frac{3}{\left(x+1\right)\left(x-1\right)}-\frac{x+3}{2.\left(x+1\right)}\right).\left(\frac{4.\left(x^2-1\right)}{5}\right)\)
\(=\frac{\left(x+1\right)^2+3.2-\left(x+3\right)\left(x-1\right)}{2.\left(x-1\right)\left(x+1\right)}.\frac{4.\left(x+1\right)\left(x-1\right)}{5}\)
\(=\frac{x^2+2x+2+6-x^2-2x+3}{2.\left(x-1\right)\left(x+1\right)}.\frac{4.\left(x+1\right)\left(x-1\right)}{5}=\frac{40.\left(x+1\right)\left(x-1\right)}{10.\left(x+1\right)\left(x-1\right)}=4\)
Vậy giá trị của biểu thức B không phụ thuộc vào biến x khi \(x\ne1;x\ne-1\)