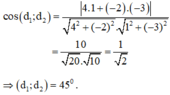Cho hai đường thẳng đenta1: 4x+3y-2=0 và đenta2: 4x+3y+1=0
Tính khoảng cách giữa đenta1 và đenta 2
Những câu hỏi liên quan
Cho điểm A(1,2,3)
đenta 1\(\left\{{}\begin{matrix}x=2-t\\y=t\\z=-1+2t\end{matrix}\right.\)
đenta 2 \(\left\{\dfrac{x+1}{1}=\dfrac{y}{1}=\dfrac{z-2}{-1}\right\}\)
a) Lập phương trình đường thẳng đenta1, đenta2 và vuông góc với mặt phẳng (P): x+y+z=0
b) Lập phương tình đường vuông góc chung của đường thẳng đenta 1 , đenta2
Tính khoảng cách giữa hai đường thẳng \({d_1}:4x - 3y + 2 = 0\) và \({d_2}:4x - 3y + 12 = 0\).
Ta thấy hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia
Chọn điểm \(A\left( {0;4} \right) \in {d_2}\), suy ra \(d\left( {{d_1},{d_2}} \right) = d\left( {A,{d_1}} \right) = \frac{{\left| {4.0 - 3.4 + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 2\)
Vậy khoảng cách giữa hai đường thẳng \({d_1}:4x - 3y + 2 = 0\) và \({d_2}:4x - 3y + 12 = 0\) là 2
Đúng 0
Bình luận (0)
Cho đường thẳng ∆: - 4x + 3y = 0. Phương trình các đường thẳng song song với ∆ và cách ∆ một khoảng bằng 3 là:
A. -4x + 3y ± 3 = 0
B. -4x + 3y ± 21 = 0
C. 4x - 3y ± 15 = 0
D. -4x + 3y ± 12 = 0
Phương trình đường thẳng song song với ∆ có dạng – 4x + 3y + c = 0. Áp dụng công thức khoảng cách giữa hai đường thẳng song song ta có
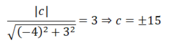
Đáp án C
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai mặt phẳng song song (P): 4x - 3y - 8 0 và (Q): 8x - 6y - 1 0. Khoảng cách giữa hai mặt phẳng (P) và (Q) là: A.
15
100
B.
3
2
C.
15
101
D.
15
28
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng song song (P): 4x - 3y - 8 = 0 và (Q): 8x - 6y - 1 = 0. Khoảng cách giữa hai mặt phẳng (P) và (Q) là:
A. 15 100
B. 3 2
C. 15 101
D. 15 28
Đáp án B
Lấy một điểm M(2 ;0 ;0)∈(P). Vì hai mặt phẳng (P) và (Q) song song nên ta có:
Đúng 0
Bình luận (0)
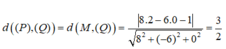
Tìm khoảng cách từ một điểm đến đường thẳng trong các trường hợp sau:
a, A(3; 5) và Δ : 4x + 3y +1 = 0
b, B(1; -2) và d: 3x – 4y -26 = 0
c, C(1; 2) và m: 3x + 4y -11 = 0
Đường thẳng d đi qua điểm M(1, 2) và song song với đường thẳng delta: 2x+3y-12=0 có phương trình tổng quát là:
a. 4x+6y+1=0 b.2x+3y-8=0
c. 4x-3y-8=0 c. 2x+3y+8=0
Xem thêm câu trả lời
trong mặt phẳng tọa độ Oxy, cho điểm M (-1;2) và đường thẳng d: 4x-3y+5=0. Tìm tọa độ điểm N thuộc đường thẳng d và cách điểm N một khoảng bằng 1
d: 4x-3y+5=0
=>VTPT là (4;-3) và (d) đi qua A(1;3)
=>VTCP là (3;4)
PTTS là:
x=1+3t và y=3+4t
=>N(3t+1;4t+3)
NM=1
=>\(\sqrt{\left(3t+1+1\right)^2+\left(4t+3-2\right)^2}=1\)
=>9t^2+12t+4+16t^2+8t+1=1
=>25t^2+20t+4=0
=>(5t+2)^2=0
=>t=-2/5
=>N(-1/5;-3/5)
Đúng 0
Bình luận (0)
Tính góc giữa hai đường thẳng
∆
:
x
-
3
y
+
2
0
và
∆
:
x
+
3
y
-
1
0
A.
90
0
B.
120
0
C.
60
0
D.
30...
Đọc tiếp
Tính góc giữa hai đường thẳng ∆ : x - 3 y + 2 = 0 và ∆ ' : x + 3 y - 1 = 0
A. 90 0
B. 120 0
C. 60 0
D. 30 0
Tính góc giữa hai đường thẳng
∆
:
x
-
3
y
+
2
0
và
∆
x
+
3
y
-
1
0
? A.
90
0
B.
120
0
C.
60
0
D. ...
Đọc tiếp
Tính góc giữa hai đường thẳng ∆ : x - 3 y + 2 = 0 và ∆ ' = x + 3 y - 1 = 0 ?
A. 90 0
B. 120 0
C. 60 0
D. 30 0
Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d1: 4x – 2y + 6 = 0 và d2: x – 3y + 1 = 0
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
Đúng 2
Bình luận (0)