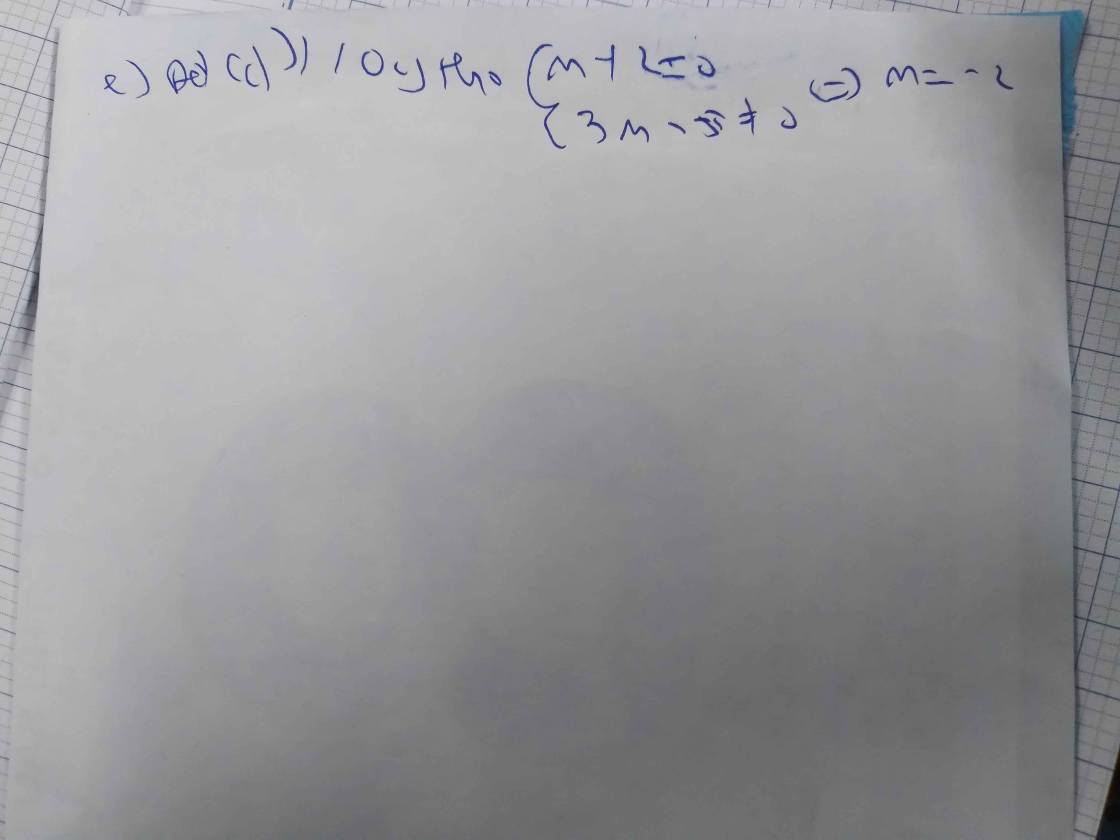tim de y =\(\frac{m-1}{m-4}\cdot x+\frac{1}{4}\) la hs dong bien

Những câu hỏi liên quan
tim m de
a,ham so y=m-2/m+2.x+3 la ham so bac nhat
b,ham so y=(5-2m)x+3m-4 la ham so dong bien
a Để đây là hàm số bậc nhất thì \(\dfrac{m-2}{m+2}< >0\)
hay \(m\notin\left\{2;-2\right\}\)
b: Để hàm số đồng biến thì 5-2m>0
=>2m<5
hay m<5/2
Đúng 0
Bình luận (0)
Cho 2 duong thang d va d' co phuong trinh lan luot la
d:y=ax+a-1
d':y=x+1
Tim cac gia tri cua a de ham so y=ax+a-1 dong bien,nghich bien
Tim gia tri cua a de:d//d'\(d\perp d'\)
2 Voi cac gia tri nao cua m thi do thi ham so y=2x+m-4 cat do thi ham so y=\(\dfrac{1}{4}x^2\) tai 2 diem phan biet
Bài 1:
a: Để hàm số đồng biến thì a>0
Để hàm số nghịch biến thì a<0
b: Để hai đường vuôg góc thì a*1=-1
=>a=-1
Bài 2:
PTHĐGĐ là:
1/4x^2=2x+m-4
=>x^2=8x+4m-16
=>x^2-8x-4m+16=0
Δ=(-8)^2-4(-4m+16)
=64+16m-64=16m
Để (P) cắt (d) tại hai điểm phân biệt thì 16m>0
=>m>0
Đúng 0
Bình luận (0)
\(y=f\left(x\right)=\left(m-1\right)x+2m-3.\)
voi m thuoc R va m khac 1. tim m de ham so tren dong bien nghich bien
tim m de ham so : y = x^3 - 3(m-1)x^2 +3m(m-2)x+2 dong bien tren cac khoang (-2;-1) va (1;2)
cho (d) y=(2tm)x+3m-5
a) tim m de ham so dong nghich bien
b) ve do thi ham so voi m=1
c ) tim m de (d) di A (3,-1)
d) tim m de (d) cat oy tai diem co tung do -2
e) tim m de (d) //OY
Moi ng giup minh.minh cam on
cho ham so y = (2m-1)x-3+m
a. tim m de ham so dong bien ?ham so nghich bien tren R ?
b.tim m de do thi ham so di qua diem E (1;20
c. ve do thi ham so voi m tim duoc o cau tren.
cho ham so y =(2m-4)x-1. Tim m de do thi ham so dong quy voi hai duong thang y = -x+1 va y=2x-5
Gia tri cua m la
\(\orbr{\begin{cases}y_1=-x+1\\y_2=2x-5\end{cases}}\Rightarrow y1=y2\Rightarrow-x+1=2x-5\Rightarrow\orbr{\begin{cases}x=2\\y1=y2=-1\end{cases}}\) A(2,-1)
y3 đi qua A=> \(\hept{\begin{cases}x=2\\y_3=-1\end{cases}\Leftrightarrow\left(2m-4\right).2-1=-1\Rightarrow m=2}\)
với m=2=> y=-1
y3 là đường thẳng // với trục hoành cắt trục tung tại (0,-1)
Đúng 0
Bình luận (0)
y = (m + 1) x -3 la ham so dong bien
\(\Leftrightarrow m+1>0\Leftrightarrow m>-1\)
Đúng 1
Bình luận (2)
cho x,y,z thuộc R, thỏa mãn \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{x+y+z}\) tính M=\(\frac{3}{4}+\left(x^2-y^2\right)\cdot\left(y^3+z^3\right)\cdot\left(z^4-x^4\right)\)
Ta có: \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=\frac{1}{x+y+z}\Leftrightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}-\frac{1}{x+y+z}=0\)
\(\Leftrightarrow\frac{x+y}{xy}+\frac{x+y+z-z}{z\left(x+y+z\right)}=0\Leftrightarrow\frac{x+y}{xy}+\frac{x+y}{z\left(x+y+z\right)}=0\)
\(\Leftrightarrow\left(x+y\right)\left(\frac{1}{xy}+\frac{1}{z\left(x+y+z\right)}\right)=0\Leftrightarrow\left(x+y\right)\left(\frac{zx+z^2+zy+xy}{xyz\left(x+y+z\right)}\right)=0\)
\(\Leftrightarrow\left(x+y\right)\left[z\left(x+z\right)+y\left(x+z\right)\right]=0\Leftrightarrow\left(x+y\right)\left(y+z\right)\left(z+x\right)=0\)
\(\Rightarrow\left(x^2-y^2\right)\left(y^3+z^3\right)\left(z^4-x^4\right)=0\).
Vậy \(M=\frac{3}{4}+\left(x^2-y^2\right)\left(y^3+z^3\right)\left(z^4-x^4\right)=\frac{3}{4}+0=\frac{3}{4}\)
Đúng 0
Bình luận (0)
1.Giải`phương trình:\(x^2-10x+27=\sqrt{6-x}+\sqrt{x-2},\)
2.Tim GTLN,GTNN cua \(A=\frac{x+1}{x^2+x+1}\)
3.Tim m de 3 duong thang dong quy :
\(d_1:y=x-4;d_2:y=2x-1;d_3:y=mx+2\)