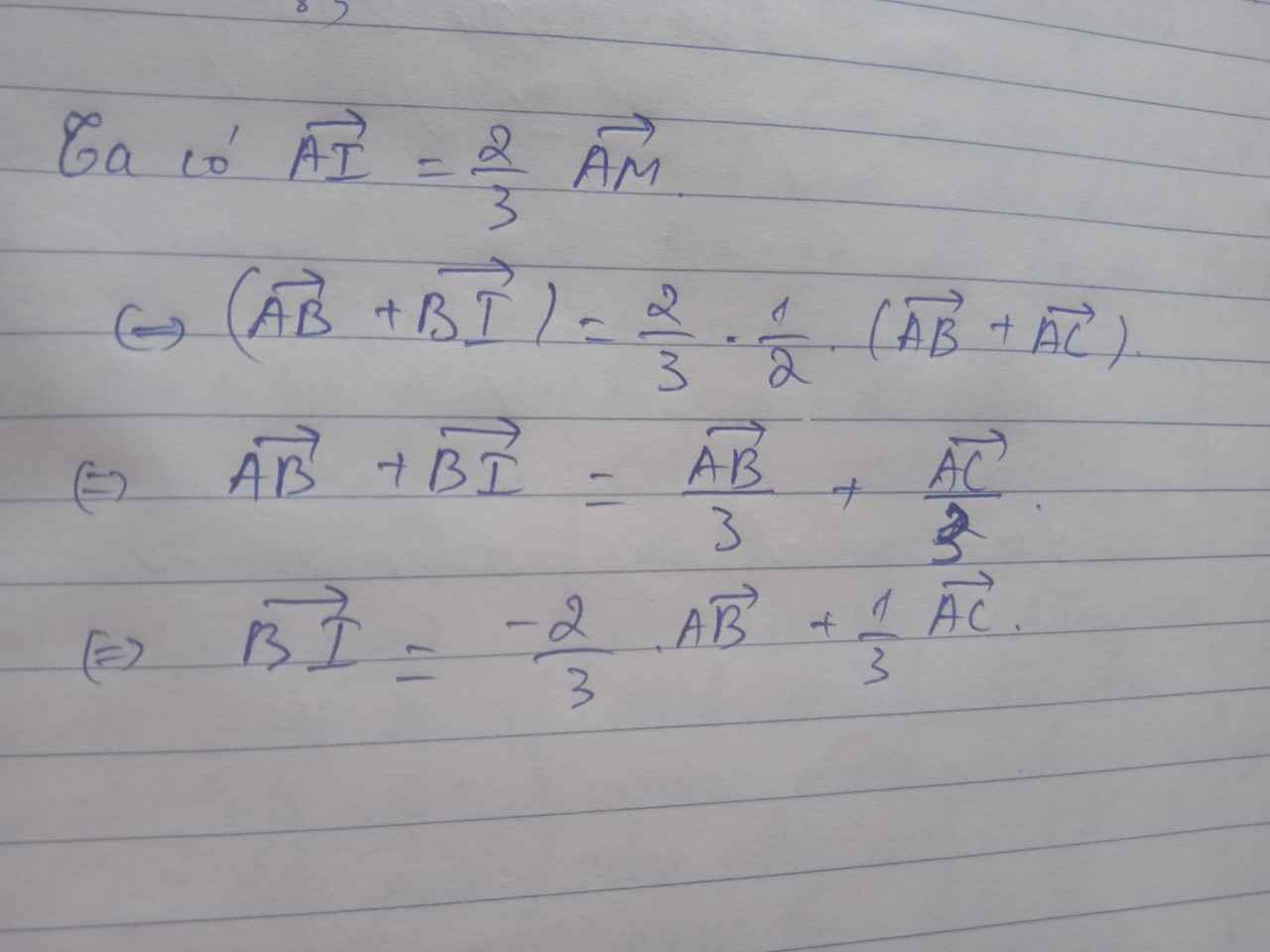Cho hình bình hành ABCD. Xác định điểm M thỏa mãn : \(3\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}\)

Những câu hỏi liên quan
Cho hình bình hành ABCD xác định. Tìm điểm M thỏa mãn \(3\overrightarrow{AM}=\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BD}\)
Cho hình bình hành ABCD tâm O. Xác định vị trí điểm M thỏa mãn \(\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{AM}\). Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, CA và dựng điểm K sao cho \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\). Khi đó, điểm K trùng với
Bài 1:
Gọi K là trung điểm của BC
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔCAB có
O,K lần lượt là trung điểm của CA,CB
=>OK là đường trung bình
=>OK//AB và \(OK=\dfrac{AB}{2}\)
=>\(\overrightarrow{OK}=\dfrac{\overrightarrow{AB}}{2}\)
=>\(\overrightarrow{AB}=2\cdot\overrightarrow{OK}\)
Xét ΔOBC có OK là đường trung tuyến
nên \(\overrightarrow{OB}+\overrightarrow{OC}=2\cdot\overrightarrow{OK}\)
=>\(\overrightarrow{AB}=\overrightarrow{OB}+\overrightarrow{OC}\)
=>M trùng với B
Bài 2:
Xét ΔABC có
M,P lần lượt là trung điểm của AB,AC
=>MP là đường trung bình của ΔABC
=>MP//BC và MP=BC/2
=>MP=CN
mà MP//NC
nên MPCN là hình bình hành
=>\(\overrightarrow{MP}=\overrightarrow{NC}\)
=>\(\overrightarrow{MP}=-\overrightarrow{CN}\)
=>\(\overrightarrow{MP}+\overrightarrow{CN}=\overrightarrow{0}\)
mà \(\overrightarrow{MK}+\overrightarrow{CN}=\overrightarrow{0}\)
nên K trùng với P
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD , gọi M là trung điểm BC, điểm I thỏa \(\overrightarrow{AI}=\dfrac{2}{3}\overrightarrow{AM}\).Chứng minh rằng \(\overrightarrow{BI}=-\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
Cho hình bình hành ABCD tâm O.Khẳng định nào sau đây sai?A, overrightarrow{AB}-overrightarrow{AD}overrightarrow{BD}B. overrightarrow{AB}+overrightarrow{AD}overrightarrow{AC}C. overrightarrow{AB}+overrightarrow{AC}2overrightarrow{AO}D. overrightarrow{OA}+overrightarrow{OB}+overrightarrow{OC}+overrightarrow{OD}overrightarrow{0}
Đọc tiếp
Cho hình bình hành ABCD tâm O.Khẳng định nào sau đây sai?
A, \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{BD}\)
B. \(\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}\)
C. \(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}\)
D. \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}\)
A sai
\(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{DA}=\overrightarrow{DA}+\overrightarrow{AB}=\overrightarrow{DB}=-\overrightarrow{BD}\) mới đúng
Đúng 2
Bình luận (0)
Cho đoạn thẳng AB = 6 cm.
a) Xác định điểm C thỏa mãn \(\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB} \)
b) Xác định điểm D thỏa mãn \(\overrightarrow {AD} = - \frac{1}{2}\overrightarrow {AB} \)
a) Ta có: \(\overrightarrow {AC} = \frac{1}{2}\overrightarrow {AB} \)
\( \Rightarrow \)Hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng hướng và \(AC = \frac{1}{2}AB\).
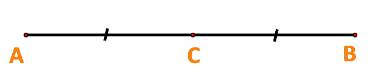
Vậy C là trung điểm của AB.
b) Ta có: \(\overrightarrow {AD} = - \frac{1}{2}\overrightarrow {AB} = - \overrightarrow {AC} \)
\( \Rightarrow \)Hai vecto \(\overrightarrow {AD} ,\overrightarrow {AC} \) ngược hướng và \(AD = AC\).
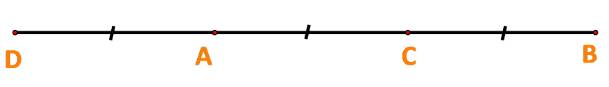
Vậy A là trung điểm DC.
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD. Gọi E là điểm thỏa mãn 4 overrightarrow{DE} overrightarrow{DC} và G là trọng tâm tam giác ABE. Đường thẳng AG cắt BC tại F. Biểu diễn overrightarrow{AG} theo overrightarrow{AB} , overrightarrow{AD} và tính tỉ số dfrac{BF}{BC}
Đọc tiếp
Cho hình bình hành ABCD. Gọi E là điểm thỏa mãn 4 \(\overrightarrow{DE}\) = \(\overrightarrow{DC}\) và G là trọng tâm tam giác ABE. Đường thẳng AG cắt BC tại F. Biểu diễn \(\overrightarrow{AG}\) theo \(\overrightarrow{AB}\) , \(\overrightarrow{AD}\) và tính tỉ số \(\dfrac{BF}{BC}\)
Cho hình bình hành ABCD . Ba điểm M,N,P thỏa mãn \(\overrightarrow{MA}+3\overrightarrow{MB},2\overrightarrow{NB}+3\overrightarrow{NC},\overrightarrow{PM}+2\overrightarrow{PN}=\overrightarrow{0}\) Phân tích vecto AP theo hai vecto \(\overrightarrow{a}=\overrightarrow{AB},\overrightarrow{b}=\overrightarrow{BD}\). Ta được
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị \(\overrightarrow {AM} \) theo hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \).
Từ M kẻ đường thẳng song song với AB, cắt AD tại E.
Khi đó tứ giác ABME là hình bình hành.
Do đó: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AE} \).
Dễ thấy: \(AE = BM = \frac{1}{2}BC = \frac{1}{2}AD\)
\( \Rightarrow \overrightarrow {AE} = \frac{1}{2}\overrightarrow {AD} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \)
Vậy \(\overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AD} \)
Chú ý khi giải
+) Dựng hình hình hành sao cho đường chéo là vecto cần biểu thị, 2 cạnh của nó song song với giá của hai vecto đang biểu thị theo.
Đúng 0
Bình luận (0)
Cho hình hình hành ABCD, gọi O là giao điểm của AC và BD. Các khảng định sau đúng hay sai?
a) \(|\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |\)
b) \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {CB} \)
c) \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \)
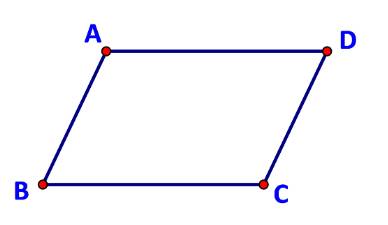
a) Theo quy tắc hình bình hành ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\( \Rightarrow |\overrightarrow {AB} + \overrightarrow {AD} |\; = \;|\overrightarrow {AC} |\)
Vậy mệnh đề này đúng.
b) Ta có: \(\overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} = \overrightarrow {BC} \ne \overrightarrow {CB} \)
Vậy mệnh đề này sai.
c) Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OC} + \overrightarrow {OD} \)\( \Leftrightarrow \overrightarrow {OA} - \overrightarrow {OD} + \overrightarrow {OB} - \overrightarrow {OC} = \overrightarrow {0} \Leftrightarrow \overrightarrow {DA} + \overrightarrow {CB} =\overrightarrow {0}\Leftrightarrow 2\overrightarrow {CB} =\overrightarrow {0} \)
Vậy mệnh đề này sai.
Đúng 0
Bình luận (0)