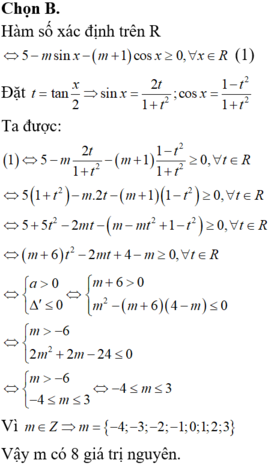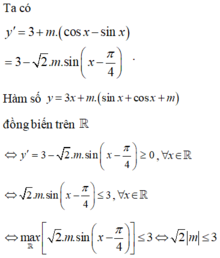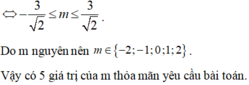cho hàm số y=cosx+msinx+1/cosx+2 (1). xác định m để GTLN của hàm số (1) trên tập R bằng 1

Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
5
-
m
sin
x
-
(
m
+
1
)
cos
x
xác định trên R? A. 6 B. 8 C. 7 D. 5
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = 5 - m sin x - ( m + 1 ) cos x xác định trên R?
A. 6
B. 8
C. 7
D. 5
Câu 1: Tìm tập xác định của hàm số y=\(\dfrac{cosx-2}{1-2sinx}\)
Câu2 : Tìm m để hàm số y=\(\sqrt{m-1+2cosx}\) xác đinh trên R
câu3 : Tìm số điểm biểu diễn nghiệm của pt: 2cos5x+1
giúp e với mn ơi
1.
Hàm số xác định khi: \(1-2sinx\ne0\Leftrightarrow sinx\ne\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x\ne\dfrac{\pi}{6}+k2\pi\\x\ne\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
2.
Đặt \(t=cosx\left(t\in\left[-1;1\right]\right)\)
Hàm số xác định trên R khi:
\(m-1+2cosx\ge0\forall x\in R\)
\(\Leftrightarrow m\ge f\left(t\right)=1-2t\forall x\in R\)
\(\Leftrightarrow m\ge maxf\left(t\right)=f\left(-1\right)=3\)
Vậy \(m\ge3\)
Đúng 0
Bình luận (0)
Xét bốn mệnh đề sau:
1
: Hàm số
y
s
inx
có tập xác định là
R
2
: Hàm số
y
c
osx
có tập xác định là
R
3
Hàm số
y
tan
x
có tập xác định là
R
4
Hàm số
y
cot...
Đọc tiếp
Xét bốn mệnh đề sau:
1 : Hàm số y = s inx có tập xác định là R
2 : Hàm số y = c osx có tập xác định là R
3 Hàm số y = tan x có tập xác định là R
4 Hàm số y = cot x có tập xác định là R
Tìm số phát biểu đúng.
A. 3
B. 2
C. 4
D. 1
Đáp án là B
• Hàm số y = sin x ; y = cos x có tập xác định D = ℝ .
• Hàm số y = tan x & y = cot x có tập xác định lần lượt D = ℝ \ π 2 + k π ; D = ℝ \ k π .
Đúng 0
Bình luận (0)
Tìm tham số m để hàm số sau xác định trên R
1/ y√cos2x+cosx−2m+1
2/ y√cos2x−2cosx+m����2�−2����+�
3/ y√sin4x+cos4x−sin2x−m
Đọc tiếp
Tìm tham số m để hàm số sau xác định trên R
1/
3/
Hàm số y
2
-
sin
2
x
m
cosx
+
1
có tập xác định R khi A. m 0 B. 0 m 1 C. m ≠ -1 D. -1 m 1
Đọc tiếp
Hàm số y = 2 - sin 2 x m cosx + 1 có tập xác định R khi
A. m > 0
B. 0 < m < 1
C. m ≠ -1
D. -1 < m < 1
Đáp án D
Hàm số có tập xác định R khi m cosx + 1 > 0, ∀x (*) .
Khi m = 0 thì (*) luôn đúng nên nhận giá trị m = 0.
Khi m > 0 thì mcosx + 1 ∈ [-m + 1; m + 1] nên (*) đúng khi -m + 1 > 0 => 0 < m < 1.
Khi m < 0 thì mcosx + 1 ∈ [m + 1; -m + 1] nên (*) đúng khi m + 1 > 0 => -1 < m < 0
Vậy giá trị m thoả mãn là -1 < m < 1.
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m để hàm số
y
3
x
+
m
sin
x
+
cos
x
+
m
đồng biến trên R? A. 3. B. Vô số. C. 4. D. 5.
Đọc tiếp
Có bao nhiêu giá trị nguyên của m để hàm số y = 3 x + m sin x + cos x + m đồng biến trên R?
A. 3.
B. Vô số.
C. 4.
D. 5.
Tìm tập xác định của hàm số sau:
\(y=\sqrt{\dfrac{1+cosx}{1-cosx}}\)
Hàm số xác định khi:
\(\left\{{}\begin{matrix}\dfrac{1+cosx}{1-cosx}\ge0\\1-cosx\ne0\end{matrix}\right.\Leftrightarrow1-cosx\ne0\Leftrightarrow cosx\ne1\Leftrightarrow x\ne k2\pi\)
Đúng 0
Bình luận (0)
tìm tất cả giá trị của m để hàm số sau có tập xác định R
a)y=\(\sqrt{m-cosx}\)
b)y=\(\sqrt{2sinx-m}\)
c)y=\(\dfrac{sinx-1}{cosx+m}\)
a.
\(\Leftrightarrow m-cosx\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge max\left(cosx\right)\)
\(\Leftrightarrow m\ge1\)
b.
\(\Leftrightarrow2sinx-m\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\le2sinx\) ; \(\forall x\)
\(\Leftrightarrow m\le\min\limits_{x\in R}\left(2sinx\right)\)
\(\Leftrightarrow m\le-2\)
c.
\(\Leftrightarrow cosx+m\ne0\) ; \(\forall x\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\max\limits_R\left(cosx\right)\\m< \min\limits_R\left(cosx\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hàm số \(y=\dfrac{2sinx+1}{\sqrt{sin^2x+\left(2m-3\right)cosx+3m-2}}\). Có bao nhiêu giá trị của m thuộc khoảng (-2023;2023) để hàm số xác định với mọi x thuộc R
Hàm số xác định trên R khi và chỉ khi:
\(sin^2x+\left(2m-3\right)cosx+3m-2>0;\forall x\in R\)
\(\Leftrightarrow-cos^2x+\left(2m-3\right)cosx+3m-1>0\)
\(\Leftrightarrow t^2-\left(2m-3\right)t-3m+1< 0;\forall t\in\left[-1;1\right]\)
\(\Leftrightarrow t^2+3t+1< m\left(2t+3\right)\)
\(\Leftrightarrow\dfrac{t^2+3t+1}{2t+3}< m\) (do \(2t+3>0;\forall t\in\left[-1;1\right]\))
\(\Leftrightarrow m>\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}\)
Ta có: \(\dfrac{t^2+3t+1}{2t+3}=\dfrac{t^2+t-2+2t+3}{2t+3}=\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}+1\)
Do \(-1\le t\le1\Rightarrow\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}\le0\)
\(\Rightarrow\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}=1\)
\(\Rightarrow m>1\)
Đúng 2
Bình luận (1)