tìm hàm số bậc nhất khi cho A( 2:3) và góc tạo bởi bằng 60 độ

Những câu hỏi liên quan
tìm hàm số bậc nhất khi cho A( 2:3) và góc tạp bởi bằng 45 độ
Bài 1: Cho hai hàm số bậc nhất: y= (k+1)x + 3 ; y= (3-2k)x + 1 a)Vẽ đồ thị của hai hàm số trên khi k=2 - Khi k=2 thì ta có hai hàm số : y= 3x+3 và y= -x+1 b) Tìm tọa độ giao điểm của đồ thị hàm số vừa vẽ. c) Tìm góc tạo bởi đường thẳng y= 3x+3 vớt trục Ox ( làm tròn đến phút ) giải giúp mik vs ak!! mik đang cần gấp lắm!!
a)
Thay x=0 vào hàm số y= 3x+3, ta được: y= 3 x 0 + 3 = 3
Thay y=0 vào hàm số y= 3x+3, ta được: 0= 3x+3 => x= -1
Vậy đồ thị hàm số đi qua điểm B(-1;0) và C(0;3)
Thay x=0 vào hàm số y= -x+1, ta được: y= -0 + 1 = 1
Thay y=0 vào hàm số y= -x+1, ta được: 0= -x+1 => x= 1
(Có gì bạn tự vẽ đồ thị nha :<< mình không load hình được sorry bạn nhiều)
b) Hoành độ giao điểm của hai đường thằng y=3x+3 và y=-x+1 :
3x+3 = -x+1
<=> 3x + x = 1 - 3
<=> 4x = -2
<=> x= - \(\dfrac{1}{2}\)
Thay x= - \(\dfrac{1}{2}\) vào hàm số y= -x+1, ta được: y= \(\dfrac{1}{2}\)+1 = \(\dfrac{3}{2}\)
Vậy giao điểm của hai đường thằng có tọa độ (\(-\dfrac{1}{2};\dfrac{3}{2}\))
c) Gọi góc tạo bởi đường thẳng y= 3x+3 là α
OB= \(\left|x_B\right|=\left|-1\right|=1\)
OC= \(\left|y_C\right|=\left|3\right|=3\)
Xét △OBC (O= 90*), có:
\(tan_{\alpha}=\dfrac{OC}{OB}=\dfrac{3}{1}=3\)
=> α= 71*34'
Vậy góc tạo bởi đường thằng y=3x+3 là 71*34'
Đúng 0
Bình luận (0)
Câu 2. (2,0 điểm) Cho hàm số bậc nhất y (a-1)x+2 (d).a) Vẽ đồ thị hàm số đã cho khi a3b) Tính góc tạo bởi đường thẳng (d) với trục Ox khi a 3 (làm tròn đến độ)c) Tìm điểm cố định mà (d) luôn đi qua .
Đọc tiếp
Câu 2. (2,0 điểm) Cho hàm số bậc nhất y= (a-1)x+2 (d).
a) Vẽ đồ thị hàm số đã cho khi a=3
b) Tính góc tạo bởi đường thẳng (d) với trục Ox khi a = 3 (làm tròn đến độ)
c) Tìm điểm cố định mà (d) luôn đi qua .
a: Thay a=3 vào (d), ta được:
y=(3-1)x+2=2x+2
*Vẽ đồ thị
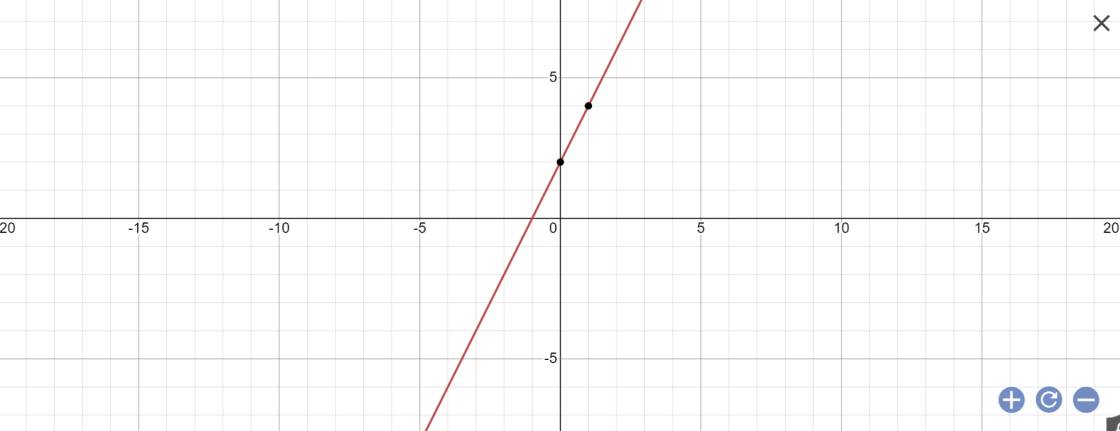
b: Gọi \(\alpha\) là góc tạo bởi đường thẳng (d): y=2x+2 với trục Ox
y=2x+2 nên a=2
\(tan\alpha=a=2\)
=>\(\alpha\simeq63^0\)
c: y=(a-1)x+2
=ax-x+2
Tọa độ điểm cố định mà (d) luôn đi qua là:
\(\left\{{}\begin{matrix}x=0\\y=-x+2=-0+2=2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y = (2m + 1)x + m – 2. Tìm m biết rằng góc tạo bởi đường thẳng và trục Ox bằng 45 ° .
A. m = 0
B. m = 1
C. m = -1
D. m = 2
Đáp án A
Vì hàm số đã cho là hàm số bậc nhất nên 2m + 1 ≠ 0 ⇔ m ≠ (-1)/2 .
Gọi góc α là góc tạo bởi đường thẳng và trục Ox . Theo giả thiết α = 45 ° . Ta có:
tan α = a ⇒ tan45 ° = 2m + 1
⇔ 1 = 2m + 1 ⇔ 0 = 2m ⇔ m = 0
Đúng 0
Bình luận (0)
Xác định hàm số bậc nhất y=ax+b trong mỗi trường hợp sau:
a) Đồ thị hàm số có hệ số góc là 2 và cắt trục tung tại điểm có tung độ bằng 2
b) Đồ thị hàm số tạo với trục hoành một góc là 60 độ và đi qua điểm B(1;-3)
a: Vì hệ số góc là 2 nên a=2
Thay x=0 và y=2 vào y=2x+b, ta được:
b+0=2
hay b=2
Đúng 1
Bình luận (1)
1a) tìm hàm số bậc nhất biết hệ số góc = -1 và đồ thị đi qua A (2 ,3)... b) vẽ đồ thị hàm số trên... c) tính góc tạo bởi đường thẳng trên và trục ox
Lời giải:
a. Giả sử đths có phương trình $y=-x+b$
Vì $A(2,3)$ đi qua đồ thị trên nên $3=-2+b$
$\Leftrightarrow b=5$
Vậy đths có phương trình $y=-x+5$
b. Cho $x=0$ thì $y=-0+5=5$
Ta có điểm $I(0,5)$ thuộc đths
Nối $I,A$ ta được đths $y=-x+5$
c.
Gọi góc tạo bởi đt và $Ox$ là $\alpha$ thì $\tan \alpha=-1$
$\Rightarrow \alpha=135^0$
Đúng 1
Bình luận (0)
Cho hàm số bậc nhất y-2x -5 (d) và y -x (d)
A. Vẽ đồ thị d và d của 2 hàm số đã cho trêb cùng 1 hệ tọa đọi Oxy
B. Tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ ( bằng phép tính)
C. Tính góc alpha tạo bởi đường thẳng d với trục hoành Ox ( làm tròn kết quả đến độ)
D. Gọi giao điểm của d với trục Oy là A, tính chu vi và diện tích tam giác MOA ( đơn vị đo trên các trục tọa độ là cm)
Đọc tiếp
Cho hàm số bậc nhất y=-2x -5 (d) và y= -x (d') A. Vẽ đồ thị d và d' của 2 hàm số đã cho trêb cùng 1 hệ tọa đọi Oxy B. Tìm tọa độ điểm M là giao điểm của 2 đồ thị vừa vẽ ( bằng phép tính) C. Tính góc alpha tạo bởi đường thẳng d với trục hoành Ox ( làm tròn kết quả đến độ) D. Gọi giao điểm của d với trục Oy là A, tính chu vi và diện tích tam giác MOA ( đơn vị đo trên các trục tọa độ là cm)
a) \(\left\{{}\begin{matrix}\left(d\right):y=-2x-5\\\left(d'\right):y=-x\end{matrix}\right.\)
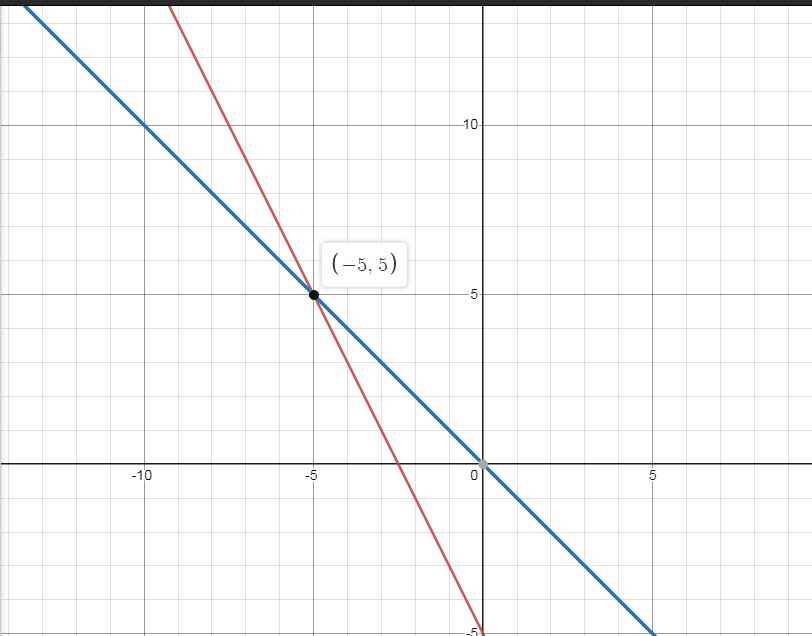
b) \(\left(d\right)\cap\left(d'\right)=M\left(x;y\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)
\(\Rightarrow M\left(-5;5\right)\)
c) Gọi \(\widehat{M}=sđ\left(d;d'\right)\)
\(\left(d\right):y=-2x-5\Rightarrow k_1-2\)
\(\left(d'\right):y=-x\Rightarrow k_1-1\)
\(tan\widehat{M}=\left|\dfrac{k_1-k_2}{1+k_1.k_2}\right|=\left|\dfrac{-2+1}{1+\left(-2\right).\left(-1\right)}\right|=\dfrac{1}{3}\)
\(\Rightarrow\widehat{M}\sim18^o\)
Đúng 0
Bình luận (0)
d) \(\left(d\right)\cap Oy=A\left(0;y\right)\)
\(\Leftrightarrow y=-2.0-5=-5\)
\(\Rightarrow A\left(0;-5\right)\)
\(OA=\sqrt[]{0^2+\left(-5\right)^2}=5\left(cm\right)\)
\(OM=\sqrt[]{5^2+5^2}=5\sqrt[]{2}\left(cm\right)\)
\(MA=\sqrt[]{5^2+10^2}=5\sqrt[]{5}\left(cm\right)\)
Chu vi \(\Delta MOA:\)
\(C=OA+OB+MA=5+5\sqrt[]{2}+5\sqrt[]{5}=5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)\left(cm\right)\)
\(\Rightarrow p=\dfrac{C}{2}=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}p-OA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5=\dfrac{5\left(\sqrt[]{2}+\sqrt[]{5}-1\right)}{2}\\p-OB=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{2}=\dfrac{5\left(-\sqrt[]{2}+\sqrt[]{5}+1\right)}{2}\\p-MA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{5}=\dfrac{5\left(\sqrt[]{2}-\sqrt[]{5}+1\right)}{2}\end{matrix}\right.\)
\(p\left(p-MA\right)=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}.\dfrac{5\left(1+\sqrt[]{2}-\sqrt[]{5}\right)}{2}\)
\(\Leftrightarrow p\left(p-MA\right)=\dfrac{25\left[\left(1+\sqrt[]{2}\right)^2-5\right]}{4}=\dfrac{25.2\left(\sqrt[]{2}-1\right)}{4}=\dfrac{25\left(\sqrt[]{2}-1\right)}{2}\)
\(\left(p-OA\right)\left(p-OB\right)=\dfrac{25\left[5-\left(\sqrt[]{2}-1\right)^2\right]}{4}\)
\(\Leftrightarrow\left(p-OA\right)\left(p-OB\right)=\dfrac{25.2\left(\sqrt[]{2}+1\right)}{4}=\dfrac{25\left(\sqrt[]{2}+1\right)}{4}\)
Diện tích \(\Delta MOA:\)
\(S=\sqrt[]{p\left(p-OA\right)\left(p-OB\right)\left(p-MA\right)}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25\left(\sqrt[]{2}-1\right)}{2}.\dfrac{25\left(\sqrt[]{2}+1\right)}{2}}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25^2}{2^2}}=\dfrac{25}{2}=12,5\left(cm^2\right)\)
Đúng 0
Bình luận (0)
| x | 0 | -5/2 | 1 |
| y=-2x-5 | -5 | 0 | |
| y=-x | 0 | -1 |
*) Đồ thị:
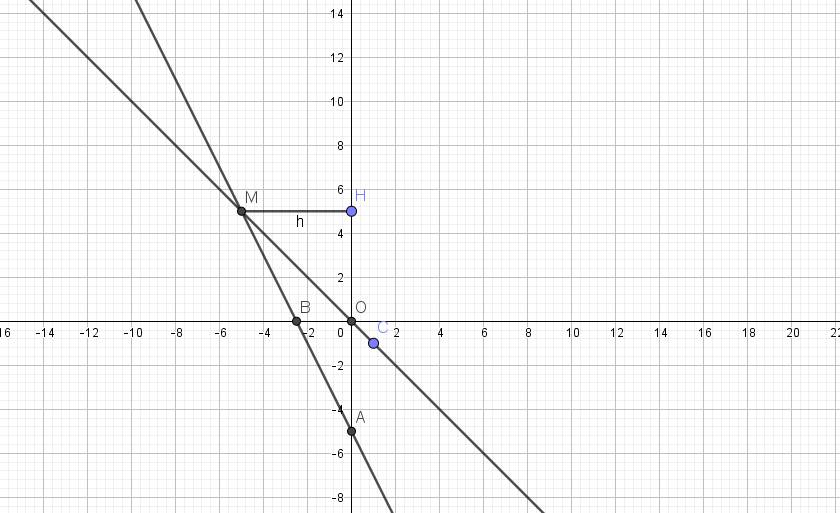
b) Phương trình hoành độ giao điểm của (d) và (d'):
\(-2x-5=-x\)
\(\Leftrightarrow-2x+x=5\)
\(\Leftrightarrow x=-5\) \(\Rightarrow y=-\left(-5\right)=5\)
Vậy tọa độ giao điểm của (d) và (d') là \(M\left(-5;5\right)\)
c) Ta có:
\(tanB=\dfrac{OA}{OB}=\dfrac{-5}{-\dfrac{5}{2}}=2\)
\(\Rightarrow\widehat{B}\simeq63^0\)
Mà góc tạo bởi d với trục hoành là \(\widehat{OBM}\)
\(\Rightarrow\widehat{OBM}\simeq180^0-63^0=117^0\)
d) Ta có:
\(OM^2=5^2+5^2=50\)
\(\Rightarrow OM=5\sqrt{2}\left(cm\right)\)
\(AM^2=5^2+10^2=125\)
\(\Rightarrow AM=5\sqrt{5}\left(cm\right)\)
Chu vi \(\Delta MOA\):
\(5\sqrt{2}+5\sqrt{5}+5=5\left(\sqrt{2}+\sqrt{5}+1\right)\left(cm\right)\)
Diện tích \(\Delta MOA\)
\(S_{MOA}=\dfrac{MH.OA}{2}=\dfrac{5.5}{2}=25\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Cho hàm số bậc nhất y=(m-2)x+m+5 . Tìm m (d) tạo với Ox 1 góc bằng 60°
Xem chi tiết
Cho 2 hàm số bậc nhất y4x-2 và y-x + 3
A. Vẽ trên cùng 1 mặt phẳng tọa độ Oxy đồ thị hai hàm số y4x -2 (d1) và y -x +3 (d2)
B. Gọi M là giao điểm của hai đường thẳng d1 và d2. Tìm tọa độ điểm M
C. Tính góc tạo bởi 2 đường thẳng d1, d2 với trục Ox (làm tròn đến phút)
D. Tìm đường thẳng d cắt d1 tại điềm A có tung độ là 6 và cắt d2 tại điểm B có hoành độ bằng nửa tung độ A. Tính chu vi và các góc tam giác AMB
Đọc tiếp
Cho 2 hàm số bậc nhất y=4x-2 và y=-x + 3 A. Vẽ trên cùng 1 mặt phẳng tọa độ Oxy đồ thị hai hàm số y=4x -2 (d1) và y= -x +3 (d2) B. Gọi M là giao điểm của hai đường thẳng d1 và d2. Tìm tọa độ điểm M C. Tính góc tạo bởi 2 đường thẳng d1, d2 với trục Ox (làm tròn đến phút) D. Tìm đường thẳng d cắt d1 tại điềm A có tung độ là 6 và cắt d2 tại điểm B có hoành độ bằng nửa tung độ A. Tính chu vi và các góc tam giác AMB
a: 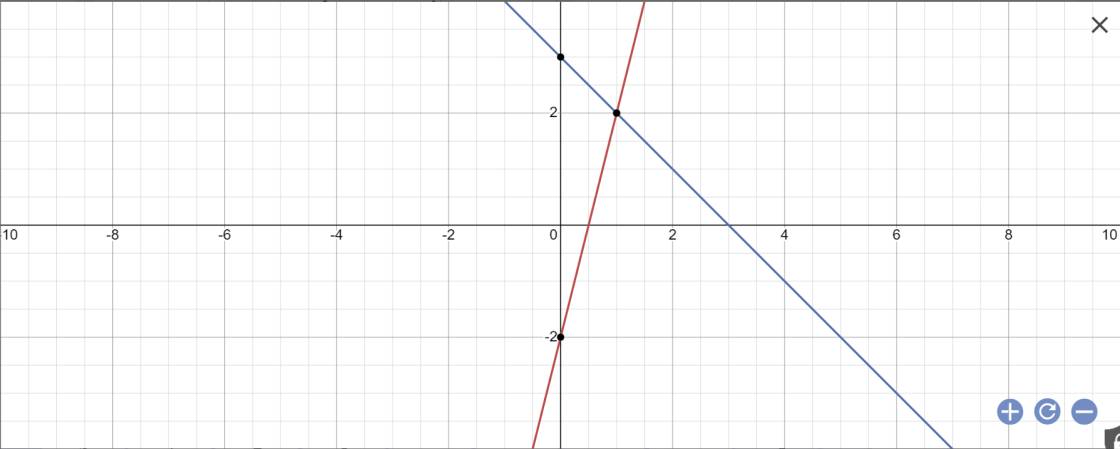
b: Phương trình hoành độ giao điểm là:
4x-2=-x+3
=>4x+x=3+2
=>5x=5
=>x=1
Thay x=1 vào y=-x+3, ta được:
\(y=-1+3=2\)
Vậy: M(1;2)
c: Gọi \(\alpha;\beta\) lần lượt là góc tạo bởi (d1),(d2) với trục Ox
(d1): y=4x-2
=>\(tan\alpha=4\)
=>\(\alpha=76^0\)
(d2): y=-x+3
=>\(tan\beta=-1\)
=>\(\beta=135^0\)
d: Thay y=6 vào (d1), ta được:
4x-2=6
=>4x=8
=>x=2
=>A(2;6)
Thay x=6/2=3 vào (d2), ta được:
\(y=-3+3=0\)
vậy: B(3;0)
Vì (d):y=ax+b đi qua A(2;6) và B(3;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+b=6\\3a+b=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+b-3a-b=6-0\\3a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-a=6\\b=-3a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=-6\\b=-3\cdot\left(-6\right)=18\end{matrix}\right.\)
Vậy: (d): y=-6x+18
e: A(2;6); B(3;0); M(1;2)
\(AM=\sqrt{\left(1-2\right)^2+\left(2-6\right)^2}=\sqrt{17}\)
\(BM=\sqrt{\left(1-3\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AB=\sqrt{\left(3-2\right)^2+\left(0-6\right)^2}=\sqrt{37}\)
Chu vi tam giác AMB là:
\(C_{AMB}=\sqrt{17}+2\sqrt{2}+\sqrt{37}\)
Xét ΔAMB có
\(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{17+8-37}{2\cdot2\sqrt{2}\cdot\sqrt{17}}=\dfrac{-3}{\sqrt{34}}\)
=>\(\widehat{AMB}\simeq121^0\) và \(sinAMB=\sqrt{1-\left(-\dfrac{3}{\sqrt{34}}\right)^2}=\dfrac{5}{\sqrt{34}}\)
Xét ΔAMB có
\(\dfrac{AB}{sinAMB}=\dfrac{AM}{sinABM}=\dfrac{BM}{sinBAM}\)
=>\(\dfrac{\sqrt{17}}{sinABM}=\dfrac{2\sqrt{2}}{sinBAM}=\sqrt{37}:\dfrac{5}{\sqrt{34}}\)
=>\(sinABM\simeq0,58;\widehat{BAM}\simeq0,4\)
=>\(\widehat{ABM}\simeq35^0;\widehat{BAM}\simeq24^0\)
Đúng 0
Bình luận (0)

















