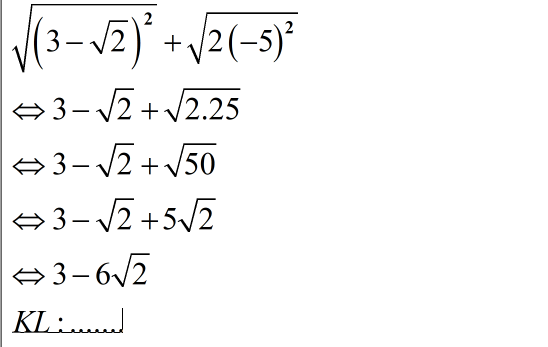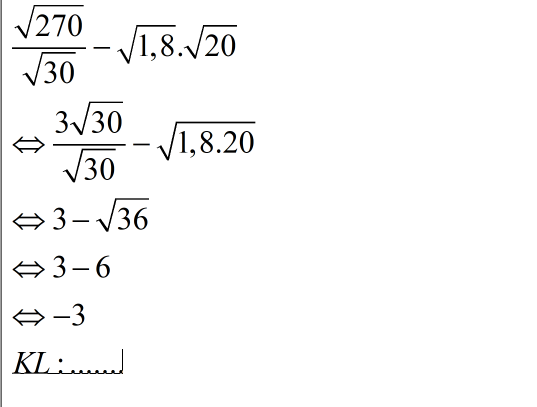`2(\sqrt{10}-\sqrt2)\sqrt{4+\sqrt{6-2\sqrt5}}`

`=2(\sqrt{10}-\sqrt2)\sqrt{4+\sqrt{(\sqrt5-1)^2}}`

`=2(\sqrt{10}-\sqrt2)\sqrt{4+\sqrt5-1}`

`=`=2(\sqrt{10}-\sqrt2)\sqrt{3+\sqrt5)`

`=2\sqrt2(\sqrt5-1)\sqrt{3+\sqrt5}`

`=2(\sqrt5-1)sqrt{6+2\sqrt5}`

`=2(\sqrt5-1)(\sqrt5+1)`

`=2(5-1)`

`=8`

`2(\sqrt{10}-\sqrt2)\sqrt{4+\sqrt{6-2\sqrt5}}`

`=2(\sqrt{10}-\sqrt2)\sqrt{4+\sqrt{(\sqrt5-1)^2}}`

`=2(\sqrt{10}-\sqrt2)\sqrt{4+\sqrt5-1}`

`=2(\sqrt{10}-\sqrt2)\sqrt{3+\sqrt5)`

`=2\sqrt2(\sqrt5-1)\sqrt{3+\sqrt5}`

`=2(\sqrt5-1)sqrt{6+2\sqrt5}`

`=2(\sqrt5-1)(\sqrt5+1)`

`=2(5-1)`

`=8`

`(4\sqrt2+\sqrt{30})(\sqrt5-\sqrt3)\sqrt{4-\sqrt{15}}`

`=\sqrt2(4+\sqrt{15})(\sqrt5-\sqrt3)\sqrt{4-\sqrt{15}}`

`=(4+\sqrt{15})(\sqrt5-\sqrt3)\sqrt{8-2\sqrt{15}}`

`=(4+\sqrt{15})(\sqrt5-\sqrt3)(\sqrt5-\sqrt3)`

`=(4+\sqrt{15})(8-2\sqrt{15})`

`=2(4+\sqrt{15})(4-\sqrt{15})`

`=2(16-15)`

`=2`

a) \(2\left(\sqrt{10}-\sqrt{2}\right)\sqrt{4+\sqrt{6-2\sqrt{5}}}\)

\(=2\left(\sqrt{10}-\sqrt{2}\right)\sqrt{4+\sqrt{5}-1}\)

\(=\dfrac{2\left(\sqrt{10}-\sqrt{2}\right)\left(\sqrt{5}+1\right)}{\sqrt{2}}\)

\(=2\cdot4=8\)

a, \(\sqrt{\left(3-\sqrt{2}\right)^2}+\sqrt{\left(2\left(-5\right)\right)^2}\)

\(=\left|3-\sqrt{2}\right|+\sqrt{\left(-10\right)^2}\)

\(=3-\sqrt{2}+\left|-10\right|\)

\(=3-\sqrt{2}+10\)

\(=13-\sqrt{2}\)

b, \(\dfrac{\sqrt{270}}{\sqrt{30}}-\sqrt{1,8}.\sqrt{20}\)

\(=\sqrt{9}-\sqrt{1,8.20}\)

\(=3-\sqrt{36}\)

\(=3-6\)

\(=-3\)

1) \(A=2\sqrt{5}-6\sqrt{2}+3\sqrt{5}=5\sqrt{5}-6\sqrt{2}\)

2) \(B=\dfrac{30\left(\sqrt{7}+1\right)}{7-1}+\dfrac{15\left(\sqrt{7}-2\right)}{7-4}=5\sqrt{7}+5+5\sqrt{7}-10=-5+10\sqrt{7}\)

3) \(C=\left(3-\dfrac{\sqrt{5}\left(\sqrt{5}-1\right)}{\sqrt{5}-1}\right)\left(3+\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\right)=\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)=9-5=4\)

4) \(D=3-\sqrt{2}+1-\sqrt{2}=4-2\sqrt{2}\)

=-5,2910456 nha bn

?? ntn

\(\left(\dfrac{\sqrt{5}-2}{\sqrt{5}+2}+1\right)\cdot\dfrac{1}{2}+\sqrt{\left(2-4\sqrt{5}\right)^2}\\ =\left(\dfrac{\sqrt{5}-2}{\sqrt{5}+2}+\dfrac{\sqrt{5}+2}{\sqrt{5}+2}\right)\cdot\dfrac{1}{2}-\left(2-4\sqrt{5}\right)\\ =\left(\dfrac{\sqrt{5}-2+\sqrt{5}+2}{\sqrt{5}+2}\right)\cdot\dfrac{1}{2}-2+4\sqrt{5}\\ =\dfrac{1}{\sqrt{5}+2}\cdot\dfrac{1}{2}-2+4\sqrt{5}\\ =\dfrac{1}{2\sqrt{5}+4}-2+4\sqrt{5}\)Tớ chỉ giúp cậu tới đây thui. Còn lại bí rồi

\(\sqrt{7-\sqrt{24}}-\dfrac{\sqrt{50}-5}{\sqrt{10}-\sqrt{5}}+\sqrt{\left(11+\sqrt{120}\right)\left(11+2\sqrt{30}\right)^2}\)

\(=\sqrt{7-2\sqrt{6}}-\dfrac{5\left(\sqrt{2}-1\right)}{\sqrt{5}\left(\sqrt{2}-1\right)}+\left|11+2\sqrt{30}\right|\sqrt{11-2\sqrt{30}}\)

\(=\sqrt{1^2-2\sqrt{6}\cdot1+\left(\sqrt{6}\right)^2}-\dfrac{\sqrt{5}\cdot\sqrt{5}}{\sqrt{5}}+\left(11+2\sqrt{30}\right)\sqrt{\left(\sqrt{6}\right)^2-2\sqrt{5}\cdot\sqrt{6}+\left(\sqrt{5}\right)^2}\)

\(=\sqrt{\left(1-\sqrt{6}\right)^2}-\sqrt{5}+\left(11+2\sqrt{30}\right)\sqrt{\left(\sqrt{6}-\sqrt{5}\right)^2}\)

\(=\left|1-\sqrt{6}\right|-\sqrt{5}+\left(11+2\sqrt{30}\right)\left|\sqrt{6}-\sqrt{5}\right|\)

\(=-1+6-\sqrt{5}+\left(\sqrt{6}+\sqrt{5}\right)^2\left(\sqrt{6}-\sqrt{5}\right)\)

\(=\sqrt{6}-1-\sqrt{5}+\left[\left(\sqrt{6}\right)^2-\left(\sqrt{5}\right)^2\right]\left(\sqrt{6}+\sqrt{5}\right)\)

\(=\sqrt{6}-1-\sqrt{5}+\left(6-5\right)\left(\sqrt{6}+\sqrt{5}\right)\)

\(=\sqrt{6}-1-\sqrt{5}+\sqrt{6}+\sqrt{5}\)

\(=2\sqrt{6}-1\)

\(=\sqrt{6+1-2\sqrt{6}}-\dfrac{\sqrt{5}\left(\sqrt{10}-\sqrt{5}\right)}{\sqrt{10}-\sqrt{5}}+\sqrt{\left(11-\sqrt{120}\right)\left(11+\sqrt{120}\right)^2}\\ =\sqrt{\left(\sqrt{6}-\sqrt{1}\right)^2}-\sqrt{5}+\sqrt{\left(11^2-120\right)\left(11+2\sqrt{30}\right)}\\ =\sqrt{6}-\sqrt{1}-\sqrt{5}+\sqrt{1\left(6+5+2\sqrt{6\cdot5}\right)}\\ =\sqrt{6}-\sqrt{1}-\sqrt{5}+\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}\\ =\sqrt{6}-\sqrt{1}-\sqrt{5}+\sqrt{6}+\sqrt{5}=2\sqrt{6}-\sqrt{1}\)

câu a

câu b

a) \(=2\sqrt{5}-3\sqrt{5}+\sqrt{5}-1=-1\)

b) \(=\left[\sqrt{14}+\dfrac{\sqrt{6}\left(\sqrt{2}+\sqrt{5}\right)}{\sqrt{2}+\sqrt{5}}\right].\sqrt{\left(\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{3}{2}}\right)^2}\)

\(=\left(\sqrt{14}+\sqrt{6}\right)\left(\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{3}{2}}\right)\)

\(=\sqrt{49}-\sqrt{21}+\sqrt{21}-\sqrt{9}\)

\(=7-3=4\)

a) \(\sqrt{20}-15\sqrt{\dfrac{1}{5}}+\sqrt{\left(1-\sqrt{5}\right)^2}=2\sqrt{5}-3\sqrt{5}+\sqrt{5}-1=-1\)

b) \(\left(\dfrac{14}{\sqrt{14}}+\dfrac{\sqrt{12}+\sqrt{30}}{\sqrt{2}+\sqrt{5}}\right).\sqrt{5-\sqrt{21}}=\left(\sqrt{14}+\sqrt{6}\right)\sqrt{5-\sqrt{21}}=\left(\sqrt{7}+\sqrt{3}\right)\sqrt{10-2\sqrt{21}}=\left(\sqrt{7}+\sqrt{3}\right)\left(\sqrt{7}-\sqrt{3}\right)=4\)