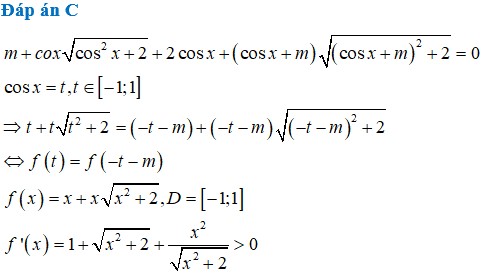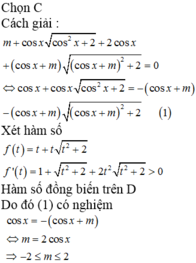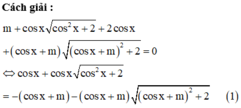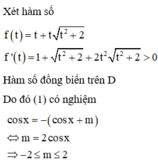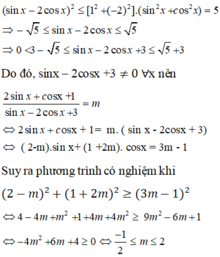Pt \(2cosx-m=cosx+1\) có nghiệm khi m nhận những giá trị trong đoạn nào?

Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên của tham số m để phương trình
m
+
c
o
s
x
c
o
s
2
x
+
2
+
2
c
o
s
x
+
(
c
o
s
x
+
m
)
(
c
o...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình m + c o s x c o s 2 x + 2 + 2 c o s x + ( c o s x + m ) ( c o s x + m ) 2 + 2 = 0 có nghiệm thực
A. 3
B. 4
C. 5
D. 6
1. Tìm tham số m để phương trình 3cos2x-7=2m có nghiệm?
2. Trên đoạn \([0;2\pi]\) , phương trình \(2cos^2x-\sqrt{3}cosx=0\)có bao nhiêu nghiệm?
3. Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số \(y=\sqrt{2cosx-3m+14}\) xác định với mọi x thuộc R?
Help me!!!
1.
\(3cos2x-7=2m\)
\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)
Phương trình đã cho có nghiệm khi:
\(-1\le\dfrac{2m-7}{3}\le1\)
\(\Leftrightarrow2\le m\le5\)
Đúng 1
Bình luận (0)
2.
\(2cos^2x-\sqrt{3}cosx=0\)
\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)
Đúng 1
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để phương trình dưới đây có nghiệm thực
m
+
cos
x
cos
2
x
+
2
+
2
cos
x
+
cos
x
+
m
cos
x
+...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình dưới đây có nghiệm thực m + cos x cos 2 x + 2 + 2 cos x + cos x + m cos x + m 2 + 2 = 0
A. 3
B. 4
C. 5
D. 6
Có bao nhiêu giá trị nguyên của tham số m để phương trình dưới đây có nghiệm thực ?
m
+
cos
x
cos
2
x
+
2
+
2
cos
x
+
cos
x
+
m
cos
x
+...
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để phương trình dưới đây có nghiệm thực ?
m + cos x cos 2 x + 2 + 2 cos x + cos x + m cos x + m 2 + 2 = 0
A. 3
B. 4
C. 5
D. 6
tìm m để pt có nghiệm
a)\(m+1=\frac{cosx}{sinx+cosx+2}\)
b) \(m=\frac{msinx-1}{2cosx-sinx+4}\)
Với giá trị nào của m thì pt \(cosx\left(2cosx-m\right)+4cosx=2m\) vô nghiệm
\(\Leftrightarrow cosx\left(2cosx-m\right)+2\left(2cosx-m\right)=0\)
\(\Leftrightarrow\left(cosx+2\right)\left(2cosx-m\right)=0\)
\(\Leftrightarrow2cosx-m=0\) (do \(cosx+2>0;\forall x\))
\(\Leftrightarrow cosx=\frac{m}{2}\)
Pt đã cho vô nghiệm khi: \(\left[{}\begin{matrix}\frac{m}{2}>1\\\frac{m}{2}< -1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để pt có nghiệm :
a. sinx - cosx = m
b. sinx - (2m-1)cosx = m+2
Phương trình
2
sin
x
+
cos
x
+
1
sin
x
-
2
cos
x
+
3
m
có nghiệm khi: A.
m
≥
2
h
o
ặ
c
m
≤
-
1...
Đọc tiếp
Phương trình 2 sin x + cos x + 1 sin x - 2 cos x + 3 = m có nghiệm khi:
A. m ≥ 2 h o ặ c m ≤ - 1 2
B. - 2 ≤ m ≤ 1 2
C. - 1 2 ≤ m ≤ 2
D. - 1 2 < m < 2
cho pt : x\(^2\)-2x+m-1=0
a)giải pt khi m =-3.
b) với giá trị nào của m thì pt có nghiệm kép ?
c) tìm m để pt có hai nghiệm mà nghiệm này gấp đôi nghiệm kia?
a. Thay m=-3 ta có: \(x^2-2x-3-1=0\Leftrightarrow x^2-2x-4=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=1+\sqrt{5}\\x=1-\sqrt{5}\end{matrix}\right.\)
b. Ta có, để phương trình có nghiệm kép thì: \(\Delta=0\Leftrightarrow2^2-4.1.\left(m-1\right)=0\Leftrightarrow m=2\)
c. Để phương trình có 2 nghiệm phân biệt thì:\(\Delta>0\Leftrightarrow2^2-4.1.\left(m-1\right)>0\Leftrightarrow m< 2\)
Áp dụng định lí Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-2\right)}{1}=2\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề ta có: \(x_1=2x_2\)\(\Rightarrow3x_2=2\Rightarrow x_2=\dfrac{2}{3}\Rightarrow x_1=\dfrac{4}{3}\Rightarrow m=\dfrac{17}{9}\)(TM)
Đúng 1
Bình luận (0)
a, Thay m = -3 vào pt trên ta được
\(x^2-2x-4=0\)
\(\Delta'=\left(-1\right)^2-\left(-4\right)=5>0\)
pt có 2 nghiệm pb
\(x_1=2-\sqrt{5};x_2=2+\sqrt{5}\)
b, Để pt có nghiệm kép
\(\Delta'=\left(-1\right)^2-\left(m-1\right)=1-m+1=2-m=0\Leftrightarrow m=2\)
Đúng 0
Bình luận (0)