Trong mặt phẳng xOy cho điểm M(9;1) . Lập phương trình đường thẳng d đi qua điểm M cắt 2 tia Ox , Oy lần lượt tại 2 điểm A,B sao cho diện tích tam giác OAB nhỏ nhất

Những câu hỏi liên quan
Trong không gian với hệ tọa độ Descartes Oxyz, cho hai điểm A(3, 2, 1) và
B
-
1
;
4
;
-
3
. Điểm M thuộc mặt phẳng (xOy) sao cho
M
A
-
M
B
lớn nhất là A.
M
-...
Đọc tiếp
Trong không gian với hệ tọa độ Descartes Oxyz, cho hai điểm A(3, 2, 1) và B - 1 ; 4 ; - 3 . Điểm M thuộc mặt phẳng (xOy) sao cho M A - M B lớn nhất là
A. M - 5 ; 1 ; 0
B. M(5, 1, 0)
C. M 5 ; - 1 ; 0
D. M - 5 ; - 1 ; 0
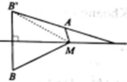
Chọn B.
Dễ thấy A, B nằm khác phía so với mặt phẳng (xOy). Gọi B’ là điểm đối xừng với B qua (xOy). Thế thì B ' - 1 ; 4 ; 3 và M B = M B ' . Khi đó
![]()
Đẳng thức xảy ra khi và chỉ khi M, A, B’ thẳng hàng và M nằm ngoài đoạn AB’. Như vậy M cần tìm là giao điểm của đường thẳng AB’ và mặt phẳng (xOy). Đường thẳng AB có phương trình
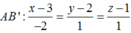
Từ đó tìm được M(5, 1, 0).
Đúng 0
Bình luận (0)
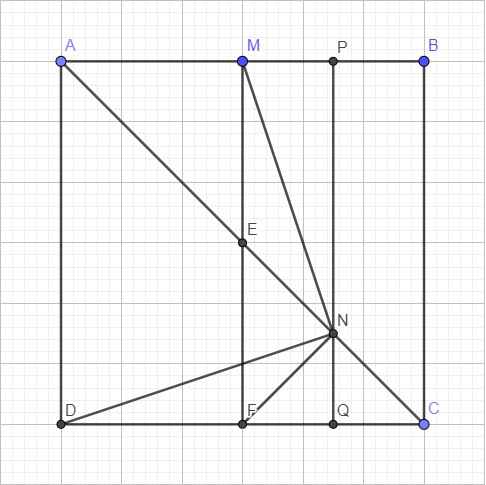
Trong mặt phẳng xOy, cho hình vuông ABCD , M là trung điểm AB,N thuộc AC sao cho AN=3NC . Viết phương tình đường thẳng CD biết M(1;2) , N(2;-1)
\(\overrightarrow{MN}=\left(1;-3\right)\Rightarrow MN=\sqrt{10}\)
Đặt \(AB=a\)
Qua N kẻ đường thẳng song song BC cắt AB và CD lần lượt tại P và Q, gọi F là trung điểm CD \(\Rightarrow MF\) song song và bằng BC
Theo Talet: \(\dfrac{PN}{BC}=\dfrac{AP}{AB}=\dfrac{AN}{AC}=\dfrac{3}{4}\Rightarrow PN=\dfrac{3a}{4}\) ; \(DQ=AP=\dfrac{3a}{4}\) ; \(MP=NQ=\dfrac{a}{4}\)
\(\Rightarrow MN^2=10=MP^2+PN^2=\dfrac{a^2}{16}+\dfrac{9a^2}{16}\Rightarrow a=4\)
\(\Rightarrow MF=4\) ; \(NQ=FQ=\dfrac{a}{4}\Rightarrow FN=\sqrt{NQ^2+FQ^2}=a\sqrt{2}\) ;
Đặt \(F\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MF}=\left(x-1;y-2\right)\\\overrightarrow{NF}=\left(x-2;y+1\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left(x-1\right)^2+\left(y-2\right)^2=MF^2=16\\\left(x-2\right)^2+\left(y+1\right)^2=FN^2=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}F\left(1;-2\right)\\F\left(\dfrac{17}{5};-\dfrac{6}{5}\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\overrightarrow{MF}=\left(0;-4\right)=-4\left(0;1\right)\\\overrightarrow{MF}=\left(\dfrac{12}{5};-\dfrac{16}{5}\right)=\dfrac{4}{5}\left(3;-4\right)\end{matrix}\right.\)
Phương trình CD:
\(\left[{}\begin{matrix}0\left(x-1\right)+1\left(y+2\right)=0\\3\left(x-\dfrac{17}{5}\right)-4\left(y+\dfrac{6}{5}\right)=0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
trong mặt phẳng xOy cho điểm M(2;3). lập pt dường thẳng d đi qua M, sao cho khoảng cách từ o(0;0) đến đường thẳng d lớn nhất
d song song voi duong thang x=y thi khoảng cách từ o(0;0) đến đường thẳng d lớn nhất
Đúng 0
Bình luận (0)
Cho gốc xOy = 110 độ . Lất điểm M trong góc xOy sao cho góc xOm = 50 độ . Trên nửa mặt phẳng bờ chứa tia Oy mà không có M lấy n sao cho góc yOn = 120 độ . Chứng tỏ rằm M,O,N thẳng hàng
B tick nếu lm đc
Trong không gian với hệ tọa độ Descartes Oxyz cho điểm M( a, b, c ). Gọi A, B, C theo thứ tự là điểm đối xứng của M qua mặt phẳng (yOz), (zOx), (xOy). Trọng tâm của tam giác ABC là A.
G
-
a
+
b
+
b
3
;
a...
Đọc tiếp
Trong không gian với hệ tọa độ Descartes Oxyz cho điểm M( a, b, c ). Gọi A, B, C theo thứ tự là điểm đối xứng của M qua mặt phẳng (yOz), (zOx), (xOy). Trọng tâm của tam giác ABC là
A. G - a + b + b 3 ; a - b + c 3 ; a + b - c 3
B. G a 3 ; b 3 ; c 3
C. G 2 a 3 ; 2 b 3 ; 2 c 3
D. G a + b + b 3 ; a + b + c 3 ; a + b + c 3
Chọn B.
Dễ thấy các điểm A, B, C có tọa độ là A(-a, b, c), B(a, -b, c), C(a, b, -c). Thế thì tọa độ trọng tâm G của tam giác ABC sẽ là G a 3 ; b 3 ; c 3
Đúng 0
Bình luận (0)
trong mặt phẳng xOy cho 3 điểm A(-1:2) B(4;-2) C(-3;-1)
tìm tọa độ của điểm M để tâm giác BCM vuông cân tại M
\(\left\{{}\begin{matrix}\overrightarrow{MB}.\overrightarrow{MC}=0\\MB=MC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[\left(x_B-x\right)\overrightarrow{i}+\left(y_B-y\right)\overrightarrow{j}\right]\left[\left(x_c-x\right)\overrightarrow{i}+\left(y_C-y\right)\overrightarrow{j}\right]=0\\\sqrt{\left(x_B-x\right)^2+\left(y_B-y\right)^2}=\sqrt{\left(x_C-x\right)^2+\left(y_C-y\right)^2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(4-x\right)\left(-3-x\right)+\left(-2-y\right)\left(-1-y\right)=0\\\left(4-x\right)^2+\left(-2-y\right)^2=\left(-3-x\right)^2+\left(-1-y\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-x+3y-10=0\\y+5=7x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\left(x-1\right)=0\\y=7x-5\end{matrix}\right.\)
\(\Rightarrow\)M(x;y): (0;-5) ; (1;2)
Đúng 0
Bình luận (0)
Trong không gian Oxyz cho điểm A (1;2;-3) và mặt phẳng (P): 2x + 2y - z + 9 0 Đường thẳng d đi qua A vuông góc với mặt phẳng (Q): 3x + 4y - 4z + 1 0 và cắt mặt phẳng (P) tại điểm B. Điểm M nằm trong (P) sao cho M luôn nhìn AB dưới góc vuông. Tính độ dài lớn nhất của MB A.
41
2
B.
5
2
C.
5
D.
41
Đọc tiếp
Trong không gian Oxyz cho điểm A (1;2;-3) và mặt phẳng (P): 2x + 2y - z + 9 = 0 Đường thẳng d đi qua A vuông góc với mặt phẳng (Q): 3x + 4y - 4z + 1 = 0 và cắt mặt phẳng (P) tại điểm B. Điểm M nằm trong (P) sao cho M luôn nhìn AB dưới góc vuông. Tính độ dài lớn nhất của MB
A. 41 2
B. 5 2
C. 5
D. 41
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
(
1
;
2
;
−
3
)
và mặt phẳng
P
:
2
x
+
2
y
−
z
+
9
0.
Đường thẳng đi qua A và vuông góc với mặt phẳng
Q
:
3
x
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A ( 1 ; 2 ; − 3 ) và mặt phẳng P : 2 x + 2 y − z + 9 = 0. Đường thẳng đi qua A và vuông góc với mặt phẳng Q : 3 x + 4 y − 4 z + 5 = 0 cắt mặt phẳng (P) tại B. Điểm M nằm trong mặt phẳng (P) sao cho M luôn nhìn đoạn AB dưới một góc vuông và độ dài MB lớn nhất. Độ dài MB là:
A. M B = 5
B. M B = 5 2
C. M B = 41 2
D. M B = 41
Đáp án A
Đường thẳng d qua A ( 1 ; 2 ; − 3 ) và vuông góc (Q) có phương trình x = 1 + 3 t y = 2 + 4 t z = − 3 − 4 t .
Vì B = d ∩ P ⇒ B 1 + 3 t ; 2 + 4 t ; − 3 − 4 t ∈ P ⇒ t = − 1 ⇒ B − 2 ; − 2 ; 1
Ta có M ∈ P M A ⊥ M B ⇒ M thuộc đường tròn giao tuyến của P và mặt cầu S (tâm I, đường kính AB)
Phương trình mặt cầu S là x + 1 2 2 + y 2 + z + 1 2 = 41 4 .
Và d I , P = 2. − 1 2 + 2.0 + 1 + 9 3 = 3
Khi đó B K = I B 2 − d 2 = 5 2 với K là tâm đường tròn giao tuyến của (P) và (S).
Để MB lớn nhất ⇔ MB là đường kính đường tròn giao tuyến ⇒ M B = 2 B K = 5 .
Đúng 0
Bình luận (0)
cho xoy=90 độ và tia oz nằm trong góc xoy , trog nửa mặt phẳng chứa tia Ox ko chứa oz vẽ góc mOx =zoy . trog nửa mặt phẳng chứa tia oy ko chứa tia oz vẽ góc yon =xoz . trên tia om đặt điểm m . trên tia on đặt điểm n và on =om . chứng minh rằng
a, on và om đối nhau
b. oz là trung trực của mn