ĐKXĐ: \(x\in R\)

\(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}=4-2x-x^2\)

=>\(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}+x^2+2x-4=0\)

\(\Leftrightarrow\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}+x^2+2x+1-5=0\)

=>\(\sqrt{3x^2+6x+7}-2+\sqrt{5x^2+10x+14}-3+\left(x+1\right)^2=0\)

=>\(\dfrac{3x^2+6x+7-4}{\sqrt{3x^2+6x+7}+2}+\dfrac{5x^2+10x+14-9}{\sqrt{5x^2+10x+14}+3}+\left(x+1\right)^2=0\)

=>

\(\dfrac{3x^2+6x+3}{\sqrt{3x^2+6x+7}+2}+\dfrac{5x^2+10x+5}{\sqrt{5x^2+10x+14}+3}+\left(x+1\right)^2=0\)

=>\(\dfrac{3\left(x^2+2x+1\right)}{\sqrt{3x^2+6x+7}+2}+\dfrac{5\left(x^2+2x+1\right)}{\sqrt{5x^2+10x+14}+3}+\left(x+1\right)^2=0\)

\(\Leftrightarrow\dfrac{3\left(x+1\right)^2}{\sqrt{3x^2+6x+7}+2}+\dfrac{5\left(x+1\right)^2}{\sqrt{5x^2+10x+14}+3}+\left(x+1\right)^2=0\)

=>\(\left(x+1\right)^2\left(\dfrac{3}{\sqrt{3x^2+6x+7}+2}+\dfrac{5}{\sqrt{5x^2+10x+14}+3}+1\right)=0\)

=>\(\left(x+1\right)^2=0\)

=>x+1=0

=>x=-1(nhận)

j kìa

x\(\in\left\{-\infty;2\frac{1}{2}-\frac{\sqrt{53}}{2}\right\}U\left\{\frac{\sqrt{53}}{2}+2\frac{1}{2};\infty\right\}\)

có bạn nào biết thì giải giúp nha , hic hic còn khảng 6 bài nữa ..........giúp nha mọi người 

=.= k biết làm thì nói toạt ra cho rồi

a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta  = 529 > 0\), có hai nghiệm phân biệt \({x_1} =  - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)

b) \( - 6{x^2} + 11x > 10 \Leftrightarrow  - 6{x^2} + 11x - 10 > 0\)

Xét tam thức \(f\left( x \right) =  - 6{x^2} + 11x - 10\) có \(\Delta  =  - 119 < 0\)và có \(a =  - 6 < 0\)

Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm

c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)

Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta  =  - 12 < 0\)và có \(a = 2 > 0\)

Ta có bảng xét dấu như sau

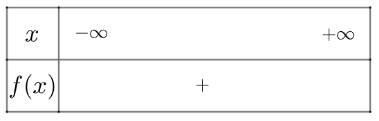
Vậy bất phương trình có vô số nghiệm

d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta  = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)

\(ĐKXĐ:5x^2+10x+1\ge0\)

\(pt\Leftrightarrow\sqrt{5\left(x^2+2x+1\right)-4}=8-\left(x^2+2x+1\right)\)

   \(\Leftrightarrow\sqrt{5\left(x+1\right)^2-4}=8-\left(x+1\right)^2\)

Đặt \(\left(x+1\right)^2=a\left(a\ge0\right)\)

\(\Rightarrow\sqrt{5a-4}=8-a\)

Bình phương lên tìm đc a rồi xem có t/m a > 0 hay ko rồi auto làm nốt

1) \(\sqrt[]{3x+7}-5< 0\)

\(\Leftrightarrow\sqrt[]{3x+7}< 5\)

\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)

\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)

\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)

Ta có : \(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+14}=-x^2-2x+4\)

Xét \(x_1< x_2< -1\), khi đó : \(f\left(x_1\right)-f\left(x_2\right)=-x_1^2-2x_1+4+x_2^2+2x_2-4=\left(x_2-x_1\right)\left(x_2+x_1+2\right)< 0\)

\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\). Vậy f(x) đồng biến với mọi \(x< -1\) 

Tương tự ta chứng minh được :

+ Với x = -1 thì VT = VP => là nghiệm của pt trên

+ Với x < -1 thì do \(f'\left(x\right)\) nghịch biến nên VT > 5 , \(f\left(x\right)\) đồng biến nên VP < 5 => vô lí

+ Với x > -1 thì do \(f'\left(x\right)\) đồng biến nên VT > 5 , \(f\left(x\right)\)nghịch biến nên VP < 5 => vô lí

Vậy x = -1 là nghiệm duy nhất của phương trình.

Ta có 

\(\sqrt{3x^2+6x+7}=\sqrt{3\left(x+1\right)^2+4}\ge2\)

\(\sqrt{5x^2+10x+14}=\sqrt{5\left(x+1\right)^2+9}\ge3\)

4 - 2x - x² = 5 - (x + 1)² \(\le5\)

Ta có VT \(\ge5\);VP \(\le\)5

Nên dấu bằng xảy ra khi x = - 1

Ta có : √3x2+6x+7+√5x2+10x+14=−x2−2x+4

Xét x1<x2<−1, khi đó : ƒ (x1)−ƒ (x2)=−x12−2x1+4+x22+2x2−4=(x2−x1)(x2+x1+2)<0

⇒ƒ (x1)<ƒ (x2). Vậy f(x) đồng biến với mọi x<−1 

Tương tự ta chứng minh được :

+ Với x = -1 thì VT = VP => là nghiệm của pt trên

+ Với x < -1 thì do ƒ '(x) nghịch biến nên VT > 5 , ƒ (x) đồng biến nên VP < 5 => vô lí

+ Với x > -1 thì do ƒ '(x) đồng biến nên VT > 5 , ƒ (x)nghịch biến nên VP < 5 => vô lí

Vậy x = -1 là nghiệm duy nhất của phương trình.

ĐKXĐ: \(x\le2\)

Xét trên miền xác định:

\(\Leftrightarrow\dfrac{2x^3+3x}{7-2x}-1+1-\sqrt{2-x}>0\)

\(\Leftrightarrow\dfrac{\left(x-1\right)\left(2x^2+2x+7\right)}{7-2x}+\dfrac{x-1}{1+\sqrt{2-x}}>0\)

\(\Leftrightarrow\left(x-1\right)\left(\dfrac{2x^2+2x+7}{7-2x}+\dfrac{1}{1+\sqrt{2-x}}\right)>0\)

\(\Leftrightarrow1< x\le2\)