\(0\le x;y;z\le2\Rightarrow\left(2-x\right)\left(2-y\right)\left(2-z\right)\ge0\)

\(\Leftrightarrow8+2\left(xy+yz+zx\right)-4\left(x+y+z\right)-xyz\ge0\)

\(\Leftrightarrow2\left(xy+yz+zx\right)\ge4+xyz\ge4\)

\(\Rightarrow xy+yz+zx\ge2\)

\(\Rightarrow Q=\left(x+y+z\right)^2-2\left(xy+yz+zx\right)\le9-2.2=5\)

\(Q_{max}=5\) khi \(\left(x;y;z\right)=\left(0;1;2\right)\) và hoán vị

*Áp dụng BĐT Svarxơ, ta có:

P\(=\frac{x^2}{1}+\frac{y^2}{1}+\frac{z^2}{1}\ge\frac{\left(x+y+z\right)^2}{3}=3\)

Vậy P_min=3\(\Leftrightarrow\frac{x^2}{1}=\frac{y^2}{1}=\frac{z^2}{1}\Rightarrow x=y=z=1\)

Gọi mặt phẳng (Q) có pt \(x+y+z-3=0\)

Gọi \(M\left(a;b;c\right)\in\left(Q\right)\) sao cho \(0\le a;b;c\le2\)

\(\Rightarrow P=OM^2=a^2+b^2+c^2\)

Bài toán trở thành tìm \(M\in\left(Q\right)\) sao cho \(OM\) đạt GTLN và GTNN

- Phần GTNN thì đơn giản rồi, gọi H là hình chiếu vuông góc của O lên (Q) \(\Rightarrow OH\perp HM\Rightarrow\) tam giác OHM vuông tại H \(\Rightarrow OH\le OM\) (trong tam giác vuông cạnh huyền luôn lớn hơn hoặc bằng cạnh góc vuông)

\(\Rightarrow OM_{min}=OH\) khi \(M\) trùng H (dễ dàng tìm ra \(H\left(1;1;1\right)\) có tọa độ thỏa mãn \(0\le a;b;c\le2\))

\(\Rightarrow OM_{min}=OH=d\left(O;\left(Q\right)\right)=\frac{\left|1.0+1.0+1.0-3\right|}{\sqrt{1+1+1}}=\sqrt{3}\Rightarrow P_{min}=OM_{min}^2=3\)

- Phần GTLN hơi phức tạp chút, có lẽ do mình ko tìm ra cách giải tốt nhất

Ta thấy M luôn nằm trong hình lập phương giới hạn bởi các mặt phẳng \(x=2;y=2;z=2\) và \(xOy;yOz;xOz\)

\(\Rightarrow M\) thuộc hình phẳng là tiết diện của \(\left(Q\right)\) với hình lập phương nói trên

\(\Rightarrow M\) thuộc hình lục giác đều có tọa độ lần lượt A(1;0;2); B(0;1;2); C(0;2;1); D(1;2;0); E(2;1;0); F(2;0;1) với tâm là \(H\left(1;1;1\right)\)

\(OM^2=OH^2+HM^2\Rightarrow OM_{max}\) khi \(HM_{max}\)

Mà \(HM\le HA=HB=HC=HD=HE=HF\)

\(\Rightarrow OM_{max}\) khi \(M\) trùng A (hoặc B, C, D, E, F)

\(\Rightarrow OM_{max}^2=OH^2+HA^2=3+\left(1-1\right)^2+\left(0-1\right)^2+\left(2-1\right)^2=5\)

\(\Rightarrow P_{max}=OM_{max}^2=5\)

Khi \(\left(x;y;z\right)=\left(1;0;2\right)\) và các hoán vị

vì trong 3 số x,y,z có ít nhất là 2 số cùng dấu

giả sử \(x,y\le0\)\(\Rightarrow z=-\left(x+y\right)\ge0\)

Mà \(-1\le x,y,z\le1\)nên \(x^2\le\left|x\right|;y^4\le\left|y\right|;z^6\le\left|z\right|\)

\(\Rightarrow x^2+y^4+z^6\le\left|x\right|+\left|y\right|+\left|z\right|=-x-y+z=-\left(x+y\right)+z=2z\le2\)

Dấu " = " xảy ra chẳng hạn x = 0 ; y = -1; z = 1

\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)

Đặt \(\dfrac{x}{y}=t\)

\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)

Với \(P=0\Leftrightarrow t=2\)

Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)

\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)

Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)

\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)

Bài a hình như sai đề rồi bạn.

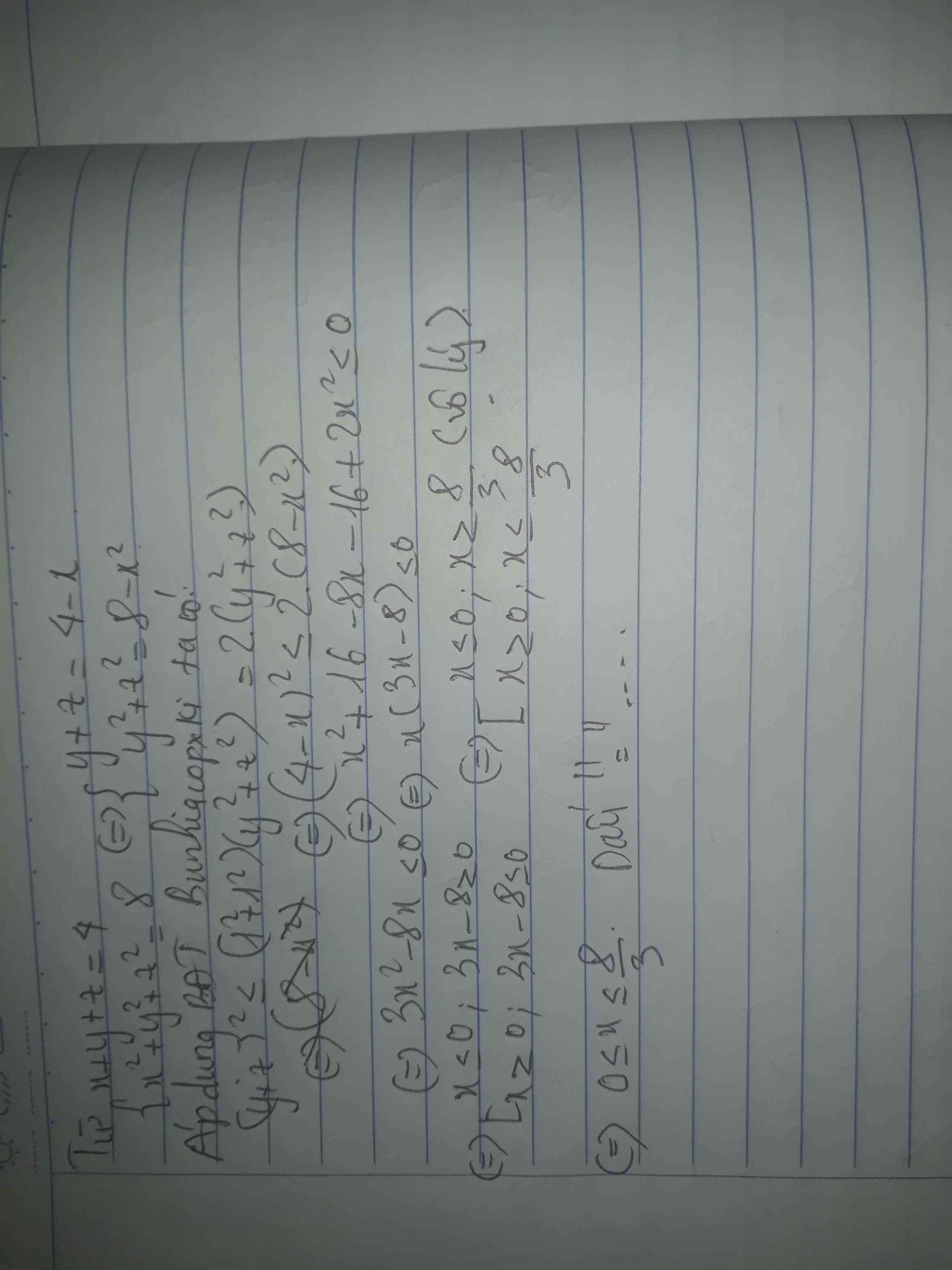
\(a,\text{Đặt }\left\{{}\begin{matrix}S=y+z\\P=yz\end{matrix}\right.\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\left(y+z\right)^2-2yz+x^2=8\\x\left(y+z\right)+yz=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S^2-2P+x^2=8\\Sx+P=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2-2\left(4-Sx\right)+x^2=8\\P=4-Sx\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2+2Sx+x^2-16=0\left(1\right)\\P=4-Sx\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\left(S+x-4\right)\left(S+x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}S=-x+4\Rightarrow P=\left(x-2\right)^2\\S=-x-4\Rightarrow P=\left(x+2\right)^2\end{matrix}\right.\)

Mà y,z là nghiệm của hệ nên \(S^2-4P\ge0\Leftrightarrow\left[{}\begin{matrix}\left(4-x\right)^2\ge4\left(x-2\right)^2\\\left(-4-x\right)^2\ge4\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)

Lời giải:

Do $x,y,z\in [0;2]\Rightarrow (x-2)(y-2)(z-2)\leq 0$

$\Leftrightarrow xyz-2(xy+yz+xz)+4(x+y+z)-8\leq 0$

$\Leftrightarrow 2(xy+yz+xz)\geq 4(x+y+z)-8+xyz$

Mà $4(x+y+z)-8+xyz=4.3-8+xyz=4+xyz\geq 4$ do $x,y,z\geq 0$

Do đó $2(xy+yz+xz)\geq 4$

Suy ra $x^2+y^2+z^2=(x+y+z)^2-2(xy+yz+xz)=9-2(xy+yz+xz)\leq 9-4=5$

Ta có đpcm. Dấu "=" xảy ra khi $(x,y,z)=(2,1,0)$ và các hoán vị.

Có nhiều cách!

Cách 2:Giả sử \(x\ge y\ge z\Rightarrow3x\ge x+y+z=3\Rightarrow2\ge x\ge1\)

Ta có: \(x^2+y^2+z^2\le x^2+y^2+2yz+z^2=x^2+\left(y+z\right)^2\)

\(=x^2+\left(3-x\right)^2=2x^2-6x+9\)

\(=2\left(x-1\right)\left(x-2\right)+5\le5\)

Đẳng thức xảy ra khi \(\left(x;y;z\right)=\left(2;1;0\right)\) và các hoán vị

Vậy...

Cách 3: Dùng khai triển Abel: Câu hỏi của Thảo Lê - Toán lớp 8 - Học toán với OnlineMath (em không chắc lắm nhưng cứ đăng)