\(c,P=\dfrac{x^2-x^2+8xy-16y^2}{x^2+4y^2}=\dfrac{8\left(\dfrac{x}{y}\right)-16}{\left(\dfrac{x}{y}\right)^2+4}\)
Đặt \(\dfrac{x}{y}=t\)
\(\Leftrightarrow P=\dfrac{8t-16}{t^2+4}\Leftrightarrow Pt^2+4P=8t-16\\ \Leftrightarrow Pt^2-8t+4P+16=0\)
Với \(P=0\Leftrightarrow t=2\)
Với \(P\ne0\Leftrightarrow\Delta'=16-P\left(4P+16\right)\ge0\)
\(\Leftrightarrow-P^2-4P+4\ge0\Leftrightarrow-2-2\sqrt{2}\le P\le-2+2\sqrt{2}\)
Vậy \(P_{max}=-2+2\sqrt{2}\Leftrightarrow t=\dfrac{4}{P}=\dfrac{4}{-2+2\sqrt{2}}=2+\sqrt{2}\)
\(\Leftrightarrow\dfrac{x}{y}=2+2\sqrt{2}\)
Bài a hình như sai đề rồi bạn.
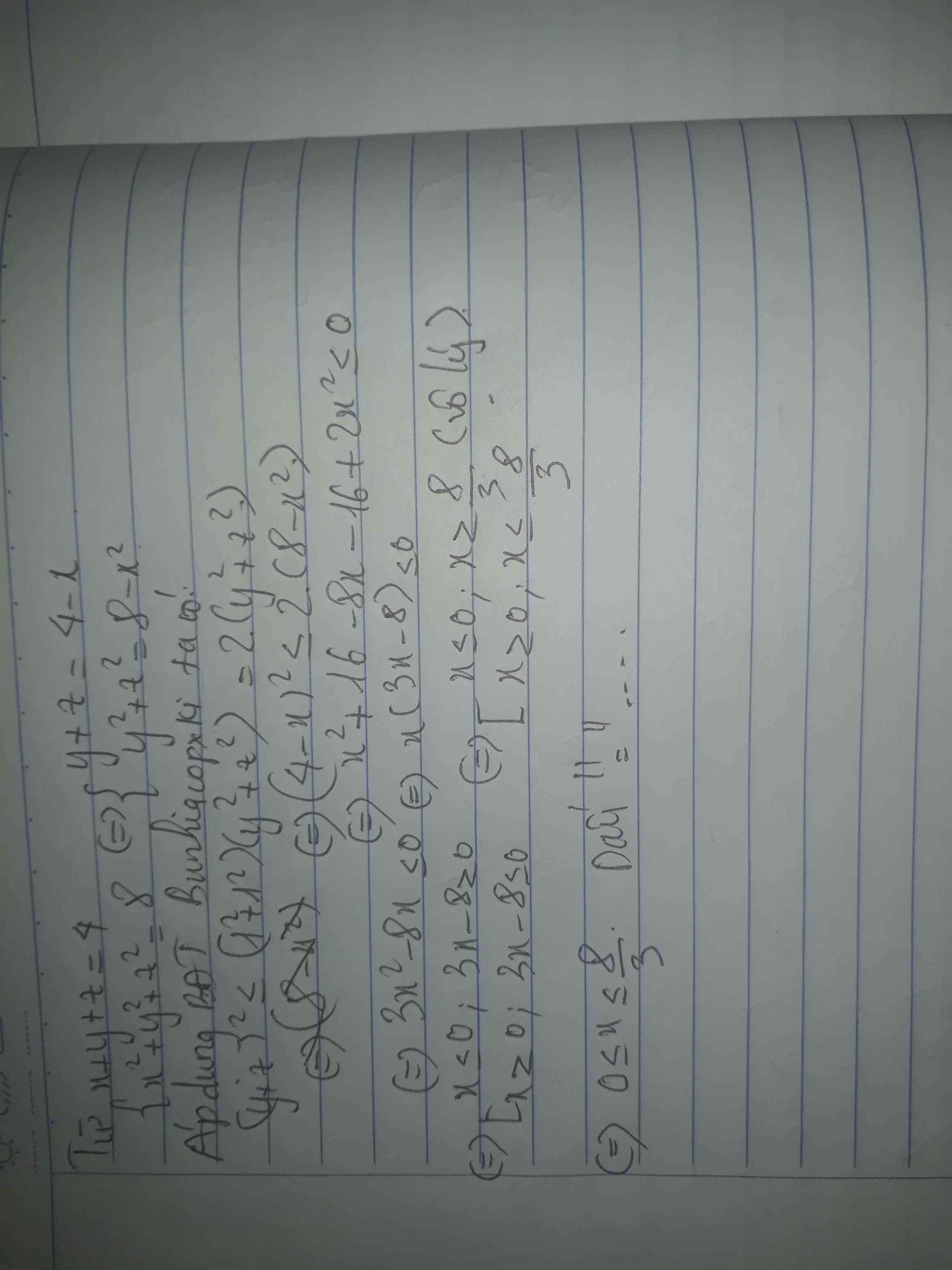
\(a,\text{Đặt }\left\{{}\begin{matrix}S=y+z\\P=yz\end{matrix}\right.\\ HPT\Leftrightarrow\left\{{}\begin{matrix}\left(y+z\right)^2-2yz+x^2=8\\x\left(y+z\right)+yz=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}S^2-2P+x^2=8\\Sx+P=4\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2-2\left(4-Sx\right)+x^2=8\\P=4-Sx\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}S^2+2Sx+x^2-16=0\left(1\right)\\P=4-Sx\end{matrix}\right.\\ \left(1\right)\Leftrightarrow\left(S+x-4\right)\left(S+x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}S=-x+4\Rightarrow P=\left(x-2\right)^2\\S=-x-4\Rightarrow P=\left(x+2\right)^2\end{matrix}\right.\)
Mà y,z là nghiệm của hệ nên \(S^2-4P\ge0\Leftrightarrow\left[{}\begin{matrix}\left(4-x\right)^2\ge4\left(x-2\right)^2\\\left(-4-x\right)^2\ge4\left(x+2\right)^2\end{matrix}\right.\Leftrightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
a.
\(8=x^2+y^2+z^2\ge x^2+2yz\Rightarrow yz\le4-\dfrac{x^2}{2}\)
\(8=x^2+y^2+z^2\ge x^2+\dfrac{1}{2}\left(y+z\right)^2=\dfrac{7x^2}{8}+\dfrac{x^2}{8}+\dfrac{1}{2}\left(y+z\right)^2\ge\dfrac{7x^2}{8}+2\sqrt{\dfrac{x^2\left(y+z\right)^2}{16}}\)
\(\Rightarrow8\ge\dfrac{7x^2}{8}+\dfrac{1}{2}x\left(y+z\right)\Rightarrow x\left(y+z\right)\le16-\dfrac{7x^2}{4}\)
Do đó:
\(4=xy+yz+zx=x\left(y+z\right)+yz\le16-\dfrac{7x^2}{4}+4-\dfrac{x^2}{2}\)
\(\Rightarrow\dfrac{9x^2}{4}\le16\Rightarrow x^2\le\dfrac{64}{9}\)
\(\Rightarrow-\dfrac{8}{3}\le x\le\dfrac{8}{3}\)
b.
\(P^2=\left(x-y\right)^2=\left(1.x-\dfrac{1}{\sqrt{3}}.\sqrt{3}y\right)^2\le\left(1+\dfrac{1}{3}\right)\left(x^2+3y^2\right)=\dfrac{4}{3}\)
\(\Rightarrow-\dfrac{2}{\sqrt{3}}\le P\le\dfrac{2}{\sqrt{3}}\)
Dấu "=" min, max lần lượt xảy ra tại \(\left(x;y\right)=\left(-\dfrac{\sqrt{3}}{2};\dfrac{\sqrt{3}}{6}\right);\left(\dfrac{\sqrt{3}}{2};-\dfrac{\sqrt{3}}{6}\right)\)















