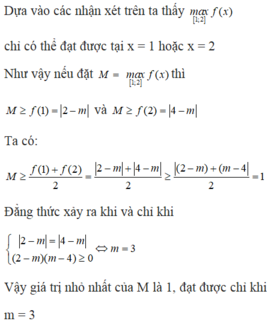Tìm giá trị lớn nhất M của hàm số f(x) = (6x+3)(5-2x) với x ∈ \(\left[\frac{-1}{2};\frac{3}{2}\right]\)

Những câu hỏi liên quan
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) \(y=f\left(x\right)=\dfrac{4}{\sqrt{5-2\cos^2x\sin^2x}}\)
b)\(y=f\left(x\right)=3\sin^2x+5\cos^2x-4\cos2x-2\)
c)\(y=f\left(x\right)=\sin^6x+\cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Cho hàm số \(y=f\left(x\right)=x^2+6x+5\). Gọi \(m,M\) lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số \(y=f\left(f\left(x\right)\right)\) với \(x\in\left[-3;0\right]\). Tính tổng \(S=m+M.\)
Ta có:
Khi \(x\in\left[-3;0\right]\) thì \(f\left(x\right)\in\left[-4;5\right]\) (dùng BBT)
Lại có:
\(y=f\left(f\left(x\right)\right)=f^2\left(x\right)+6f\left(x\right)+5\)
Khi \(f\left(x\right)\in\left[-4;5\right]\) thì \(f\left(f\left(x\right)\right)\in\left[-4;60\right]\) (dùng BBT)
Do đó, \(m=-4\Leftrightarrow f\left(x\right)=-3\Leftrightarrow x=-2\)
và \(M=60\Leftrightarrow f\left(x\right)=5\Leftrightarrow x=0\)
\(\Rightarrow S=m+M=-4+60=56\)
Đúng 2
Bình luận (0)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
a) y=f(x)=\(\dfrac{4}{\sqrt{5-2cos^2xsin^2x}}\)
b)y=f(x)=\(3sin^2x+5cos^2x-4cos2x-2\)
c)y=f(x)=\(sin^6x+cos^6x+2\forall x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)
Cho hàm số \(y=f\left(x\right)=x^2+2\left(m-1\right)x+3m-5\) (m là tham số). Tìm m để giá trị nhỏ nhất của f(x) đạt giá trị lớn nhất
Dễ thấy: \(f\left(x\right)=\left(x+m-1\right)^2-m^2+5m-6\ge-m^2+5m-6\)
Giá trị nhỏ nhất của f(x) đạt lớn nhất tức \(-m^2+5m-6\) đạt lớn nhất
Mà \(g\left(m\right)=-m^2+5m-6=-\left(m-\dfrac{5}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
g(m) đạt lớn nhất khi m=5/2
m cần tìm là 5/2
Đúng 0
Bình luận (0)
Cho hàm số f(x) = \(\left\{{}\begin{matrix}-x+1khix< -2\\2x+7khix\ge-2\end{matrix}\right.\)
a) Lập bảng biến thiên và vẽ đồ thị hàm số trên
b) Tìm m để phương trình f(x)=m có 2 nghiệm phân biệt
c) Tìm giá trị lớn nhất, nhỏ nhất của hàm số trên [-3; 1]
tìm giá trị lớn nhất của hàm số : \(f\left(x\right)=\frac{x^2}{x^2-2x+2016}\)
Ta có : f(x) đạt giá trị lớn nhất <=> \(\frac{1}{f\left(x\right)}\) đạt giá trị nhỏ nhất
Xét : \(\frac{1}{f\left(x\right)}=\frac{x^2-2x+2016}{x^2}=\frac{2016}{x^2}-\frac{2}{x}+1\)
Đặt \(t=\frac{1}{x}\Rightarrow\frac{1}{f\left(x\right)}=2016t^2-2t+1=2016\left(t-\frac{1}{2016}\right)^2+\frac{2015}{2016}\ge\frac{2015}{2016}\)
\(\frac{1}{f\left(x\right)}\) đạt giá trị nhỏ nhất bằng \(\frac{2015}{2016}\)
Suy ra f(x) đạt giá trị lớn nhất bằng \(\frac{2016}{2015}\)
Dấu đẳng thức xảy ra khi và chỉ khi \(t=\frac{1}{2016}\Leftrightarrow x=2016\)
Đúng 0
Bình luận (0)
Cho hàm số \(f\left(x\right)=\dfrac{x-m^2}{x+8}\)với m là tham số cực . Tìm giá trị lớn nhất của m để hàm số có giá trị nhỏ nhất trên đoạn \(\left[0;3\right]=2\)
f'(x)>0 với mọi x khác -8, suy ra hàm số đã cho đồng biến trên [0;3].
Giá trị nhỏ nhất của f(x) trên [0;3] là (-m^2)/8. Ta có: (-m^2)/8=2.
Suy ra, không có giá trị nào của số thực m thỏa yêu cầu đề bài.
Đúng 0
Bình luận (3)
Cho hàm số f(x) = |2x − m|. Tìm m để giá trị lớn nhất của f(x) trên [1; 2] đạt giá trị nhỏ nhất.
A. m = −3
B. m = 2
C. m = 3
D. m = −2
1. Tìm giá trị lớn nhất của biểu thức 7lx-3l-l4x+8l-l2-3xl2. Cho hàm số f(x) xác định với mọi x varepsilonQ. Cho f(a+b) f(a.b) với mọi a, b và f(2011) 11. Tìm f(2012)3.Cho hàm số f thỏa mãn f(1) 1; f(2) 3; f(n) +f(n+2) 2f(n+1) với mọi số nguyên dương n. Tính f(1) + f(2) + f(3)+...+f(30)4. Tính giá trị của biểu thức left(frac{3}{4}-81right)left(frac{^{3^2}}{5}-81right)left(frac{3}{6}^3-81right)...left(frac{3}{2014}^{2011}-81right)5. Đa thức P(x) cộng với đa thức Q(x) x^3-2x^2-1 được đa thức ^...
Đọc tiếp
1. Tìm giá trị lớn nhất của biểu thức 7lx-3l-l4x+8l-l2-3xl
2. Cho hàm số f(x) xác định với mọi x \(\varepsilon\)Q. Cho f(a+b) =f(a.b) với mọi a, b và f(2011) = 11. Tìm f(2012)
3.Cho hàm số f thỏa mãn f(1) =1; f(2) = 3; f(n) +f(n+2) = 2f(n+1) với mọi số nguyên dương n. Tính f(1) + f(2) + f(3)+...+f(30)
4. Tính giá trị của biểu thức \(\left(\frac{3}{4}-81\right)\left(\frac{^{3^2}}{5}-81\right)\left(\frac{3}{6}^3-81\right)...\left(\frac{3}{2014}^{2011}-81\right)\)
5. Đa thức P(x) cộng với đa thức Q(x) = \(x^3-2x^2-1\) được đa thức \(^{x^2}\). Tìm hệ số tự do của P(x)
6. Cho a, b, c là các số thỏa mãn điều kiện \(\frac{2a-b}{a+b}=\frac{b-a+c}{2a-3}=\frac{2}{3}\). Tính \(\frac{\left(5b+4a\right)^5}{\left(5b+4a\right)^2\left(a+3c\right)^3}\)
4. (3/4-81)(3^2/5-81)(3^3/6-81)....(3^6/9-81).....(3^2011/2014-81)
mà 3^6/9-81=0 => (3/4-81)(3^2/5-81)....(3^2011/2014-81)=0
Đúng 0
Bình luận (0)