Khai triển hàm số đến mức tối giản nhất
Y=4cosx.cos5x.sin6x
Những câu hỏi liên quan
Cho hàm số
y
tan
3
x
−
1
c
o
s
2
x
+
2
. Giá trị nhỏ nhất của hàm số trên
0
;
π
2
là phân số tối giản
a
b
, ở đ...
Đọc tiếp
Cho hàm số y = tan 3 x − 1 c o s 2 x + 2 . Giá trị nhỏ nhất của hàm số trên 0 ; π 2 là phân số tối giản a b , ở đó a , b là số nguyên và b > 0 . Tính hiệu a − b .
A. 50
B. - 4
C. 4
D. - 50
rút gọn phân số đến mức tối giản
121212
131313 = ?
\(\frac{121212}{131313}=\frac{12.10101}{13.10101}=\frac{12}{13}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
10 tháng 1 2022 lúc 15:49
Biết giá trị nhỏ nhất của hàm số y = |3x−1| + |x+1| là a/b với a, b thuộc N* và a/b tối giản. Tính a+b.
Gọi M là giá trị lớn nhất của hàm số
y
2
3
x
3
−
2
x
2
+
1
trên
−
8
3
;
3
.
Biết...
Đọc tiếp
Gọi M là giá trị lớn nhất của hàm số y = 2 3 x 3 − 2 x 2 + 1 trên − 8 3 ; 3 . Biết M = a b với a b là phân số tối giản a ∈ Z , b ∈ N * . Tính S = a + b 3 .
A. S = 32.
B. S = 128.
C. S = 3.
D. S = 2.
Đáp án A.
Lưu ý: Nếu c, d lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = f x trên (m;n) thì giá trị lớn nhất của hàm số y = f x trên (m;n) là M a x a ; b .
Xét hàm số f x = 2 3 x 3 − 2 x 2 + 1. Ta có f ' x = 2 x 3 − 4 x = 2 x x − 2 . Ta có bảng biến thiên của hàm số trên − 8 3 ; 3 như sau:
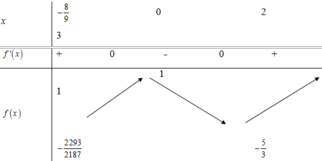
Dựa vào bảng biến thiên, ta thấy M i n f x = − 5 3 và M a x f x = 1 trên − 8 3 ; 3 .
Do đó
M = M a x − 5 3 ; 1 = 5 3 ⇒ a = 5 ; b = 3.
Do đó S = a + b 3 = 5 + 3 3 = 32.
Đúng 0
Bình luận (0)
Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?
a) \(y = 2x(x - 3)\)
b) \(y = x({x^2} + 2) - 5\)
c) \(y = - 5(x + 1)(x - 4)\)
a) \(y = 2x(x - 3) = 2{x^2} - 6\)
Hàm số có lũy thừa bậc cao nhất của x là bậc hai
b) \(y = x({x^2} + 2) - 5 = {x^3} + 2x - 5\)
Hàm số có lũy thừa bậc cao nhất của x là bậc ba
c) \(y = - 5(x + 1)(x - 4) = - 5{x^2} + 15x + 20\)
Hàm số có lũy thừa bậc cao nhất của x là bậc hai
Đúng 0
Bình luận (0)
Cho hàm số 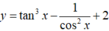. Giá trị nhỏ nhất của hàm số trên là phân số tối giản
a
b
, ở đó a,b là số nguyên và b 0. Tính hiệu a-b. A. 50 B. -4 C. 4 D. -50
Đọc tiếp
Cho hàm số 
. Giá trị nhỏ nhất của hàm số trên 
là phân số tối giản
a
b
, ở đó a,b là số nguyên và b > 0. Tính hiệu a-b.
A. 50
B. -4
C. 4
D. -50
Gọi
m
0
là giá trị nhỏ nhất của tham số thực m để hàm số
y
x
3
+
3
x
2
+
m
x
+
m
nghịch biến trên một đoạn có độ dài bằng 1. Biết rằng
m
0
a
b
,
a
∈
ℕ
,
b
∈...
Đọc tiếp
Gọi m 0 là giá trị nhỏ nhất của tham số thực m để hàm số y = x 3 + 3 x 2 + m x + m nghịch biến trên một đoạn có độ dài bằng 1. Biết rằng m 0 = a b , a ∈ ℕ , b ∈ ℕ * và a b là phân số tối giản. Tính P = a b + a − b
A. P = 49
B. P = 41
C. P = 47
D. P = 36
Cho biết tập xác định của hàm số
y
log
1
2
(
-
1
+
log
1
4
x
)
là một khoảng có độ dài
m
n
(phân số tối giản). Tính giá trị m + n. A. 6 B. 5 C. 4 D. 7
Đọc tiếp
Cho biết tập xác định của hàm số y = log 1 2 ( - 1 + log 1 4 x ) là một khoảng có độ dài m n (phân số tối giản). Tính giá trị m + n.
A. 6
B. 5
C. 4
D. 7
Cho biết tập xác định của hàm số
y
log
1
2
-
1
+
log
1
4
x
là một khoảng có độ dài
m
n
(phân số tối giản). Tính giá trị m + n. A. 6 B. 5 C. 4 D. 7
Đọc tiếp
Cho biết tập xác định của hàm số y = log 1 2 - 1 + log 1 4 x là một khoảng có độ dài m n (phân số tối giản). Tính giá trị m + n.
A. 6
B. 5
C. 4
D. 7
Đáp án B
x > 0 - 1 + log 1 4 x > 0 ⇔ x > 0 log 1 4 x > 1 ⇔ x > 1 4 ⇒ m = 1 m = 4 ⇒ m + n = 5
Đúng 0
Bình luận (0)