Các câu hỏi tương tự
Kí hiệu a, b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x) sin2x + 2sinx trên đoạn . Giá trị a +b bằng
Đọc tiếp
Kí hiệu a, b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f (x) = sin2x + 2sinx trên đoạn 
. Giá trị a +b bằng
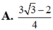
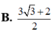
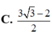
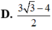
Kí hiệu a,b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
f
x
sin
2
x
+
2
sin
x
trên đoạn
0
;
3
π
2
. Giá trị a+b bằng
Đọc tiếp
Kí hiệu a,b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f x = sin 2 x + 2 sin x trên đoạn 0 ; 3 π 2 . Giá trị a+b bằng
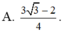
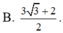
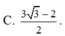
Cho hàm số f(n) 1+3+6+10+...+
n
(
n
+
1
)
2
(
n
∈
N
*
)
. Biết lim
f
(
n
)
(
3
n
+
1
)...
Đọc tiếp
Cho hàm số f(n)= 1+3+6+10+...+ n ( n + 1 ) 2 ( n ∈ N * ) .
Biết lim f ( n ) ( 3 n + 1 ) ( 5 n 2 + 2 ) = a b ( a , b ∈ Z ) phân số này tối giản. Giá trị b - 5a là
A.50
B.45
C.85
D.60
Biết
lim
x
→
0
3
x
+
1
-
1
x
a
b
, trong đó a,b là các số nguyên dương và phân số
a
b
tối giản. Tính giá trị biểu thức...
Đọc tiếp
Biết lim x → 0 3 x + 1 - 1 x = a b , trong đó a,b là các số nguyên dương và phân số a b tối giản. Tính giá trị biểu thức P = a 2 + b 2 .
A.P=13.
B.P= 0.
C. P=5.
D. P=40
Biết
lim
x
→
-
∞
x
+
1
2
x
+
1
5
x
3
+
x
+
2...
Đọc tiếp
Biết lim x → - ∞ x + 1 2 x + 1 5 x 3 + x + 2 = - a b trong đó a, b là các số nguyên dương và a b là phân số tối giản. Giá trị của tích ab bằng.
A. 30
B. 42
C. 10
D. 36
Biết
lim
x
→
∞
(
x
+
1
)
2
x
+
1
5
x
3
+
x
+
2
-...
Đọc tiếp
Biết lim x → ∞ ( x + 1 ) 2 x + 1 5 x 3 + x + 2 = - a b trong đó a, b là các số nguyên dương và a b là phân số tối giản. Giá trị của tích ab bằng
A.30
B.42
C.10
D.36
Biết \(\lim\limits_{x->+\infty}\) \(\left(\sqrt{25x^2+4\sqrt{2}+5}-5x\right)=\dfrac{a\sqrt{b}}{c}\) trong đó a,b,c là các số nguyên duơng, phân số \(\dfrac{a}{c}\) tối giản và \(a>1\). Tính \(S=a^2+b^2+c^2\)
Cho hàm số yf(x) và yg(x) là hai hàm liên tục trên
ℝ
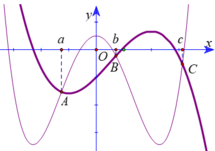
có đồ thị hàm số y f (x) là đường cong nét đậm và y g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của yf (x) và yg(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) f(x) - g(x) trên đoạn [a;c]?
Đọc tiếp
Cho hàm số y=f(x) và y=g(x) là hai hàm liên tục trên ℝ có đồ thị hàm số y = f '(x) là đường cong nét đậm và y = g(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A,B,C của y=f '(x) và y=g'(x) trên hình vẽ lần lượt có hoành độ a.b.c. Tìm giá trị nhỏ nhất của hàm số h(x) = f(x) - g(x) trên đoạn [a;c]?
Cho a,b là các số thực và hàm số
f
x
x
-
a
-
1
x
2
-
4...
Đọc tiếp
Cho a,b là các số thực và hàm số f x = x - a - 1 x 2 - 4 k h i x ≠ 2 2 x - b k h i x = 2 liên tục tại x=2. Tính giá trị của biểu thức T=a+b.
A. T= 31 8
B. T=5
C. T=3
D. T= 39 8