Cho tam giác ABC cân tại A nội tiếp đường tròn (O; R) (A^<90độ). Gọi H, I lần lượt là trung điểm AB và AC. Nối OH, OI cắt các cung nhỏ AB, AC lần lượt tại M và N.
a) Chứng minh OA⊥MN
b) Tam giác ABC phải có thêm điều kiện gì để OMAN là hình thoi?
Những câu hỏi liên quan
Cho tam giác ABC cân tại A nội tiếp đường tròn (O) , cạnh bên bằng b. Tính bán kính đường tròn nội tiếp tam giác
cho tam giác abc nội tiếp đường tròn (o), I là tâm đường tròn nội tiếp tam giác abc. AI cắt (o) tại M, c/m tam giác MIB cân
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh AB = a, đường cao AH = h. Tính
bán kính đường tròn ngoại tiếp tam giác theo a và h.
Cho tam giác ABC cân tại A nội tiếp đường tròn O đường kính AI gọi E là trung điểm của AB K là trung điểm của OI
a, CMR: tam giác EKB cân
b, tứ giác AEKC nội tiếp đường tròn
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh bên bằng b, đường cao
AH=h. Tính bán kính đường tròn (O).
Kéo dài AH cắt đường tròn tại D \(\Rightarrow\) AD là đường kính
\(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn hay tam giác ABD vuông tại B
Áp dụng hệ thức lượng:
\(AB^2=AH.AD\Rightarrow AD=\dfrac{AB^2}{AH}=\dfrac{b^2}{h}\)
\(\Rightarrow2R=\dfrac{b^2}{h}\Rightarrow R=\dfrac{b^2}{2h}\)
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn nội tiếp đường tròn (O). Hai đường cao AM ,BN cắt nhau tại H và cắt đường tròn (O) lần lượt tại D,E. chứng minh rằng
a. tứ giác HMCN nội tiếp đường tròn
b. CD=CE
c. tam giác BHD cân
a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CAD=góc NBC
=>1/2*sđ cung CD=1/2*sđ cung CE
=>CD=CE
c: góc BHM=góc BCN=1/2*sđ cung BA
góc BDH=1/2*sđ cung BA
=>góc BHD=góc BDH
=>ΔBHD cân tại B
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh bên bằng 10a, đường cao AH bằng
8a. Tính bán kính đường tròn (O).
Kẻ đường kính AD thì góc ACD = 90°
Ta có AC²= AD.AH nên AD = AC²/AH
<=>AD= (10a)²/ 8a=100a/8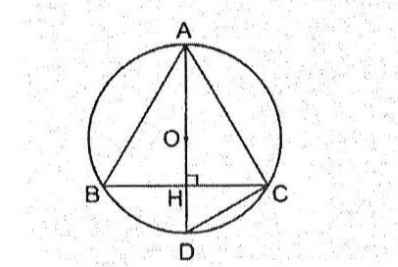
Đúng 1
Bình luận (0)
cho đường tròn tâm o nội tiếp tam giác ABC cân tại A đường cao AH cắt đường tròn tâm o tại D chứng minh BC.BC=4AH.DH
các bạn giúp mình nhé sáng thứ tư mình nộp bài rồi cảm ơn
Đúng 0
Bình luận (0)
5 tháng 2 2022 lúc 9:55
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Khi đó tỉ số \(\dfrac{R}{r}\) bằng
Giải chi tiết cho mk vs
Tham khảo:
Ta có: \(R=\dfrac{abc}{4S};r=\dfrac{S}{p}\)
Vì tam giác ABC vuông cân tại A nên \(b=c\) và \(a=\sqrt{b^2+c^2}=b\sqrt{2}\)
Xét tỉ số:
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}.\left(b.c\right)^2}=\dfrac{a\left(a+2b\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)
Đúng 0
Bình luận (3)
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}\left(b.c\right)^2}=\dfrac{a.b^2\dfrac{\left(a+2b\right)}{2}}{b^4}=\dfrac{a.b^2\left(a+2b\right)}{2b^4}=\dfrac{a\left(a+2b\right)}{2b^2}\)
\(=\dfrac{b\sqrt{2}\left(b\sqrt{2}+2b\right)}{2b^2}=\dfrac{b^2\sqrt{2}\left(\sqrt{2}+2\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)
Đúng 3
Bình luận (1)
Cho tam giác ABC cân tại A, đ tròn (O) ngoại tiếp tam giác ABC, đường tròn tâm (O') tiếp xúc trong với (O) và tiếp xúc với cạnh AB ở P, AC ở Q. Cm trung điểm I của PQ là tâm đ tròn nội tiếp tam giác ABC