Tam thức \(f\left( x \right) = 2{x^2} - 5x + 3\) có \(\Delta  = 1 > 0\), hai nghiệm phân biệt là \({x_1} = 1,{x_2} = \frac{3}{2}\) và \(a = 2 > 0\)

Ta có bảng xét dấu như sau:

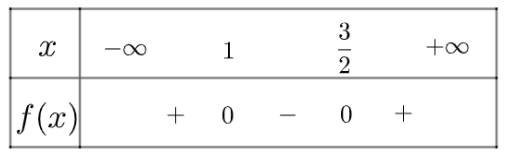
Vậy tam thức đã cho mang dấu dương khi x nằm trong khoảng \(\left( { - \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)

Answer:

a) \(\frac{5x}{2x+2}+1=\frac{6}{x+1}\)

\(\Rightarrow\frac{5x}{2\left(x+1\right)}+\frac{2\left(x+1\right)}{2\left(x+1\right)}=\frac{12}{2\left(x+1\right)}\)

\(\Rightarrow5x+2x+2-12=0\)

\(\Rightarrow7x-10=0\)

\(\Rightarrow x=\frac{10}{7}\)

b) \(\frac{x^2-6}{x}=x+\frac{3}{2}\left(ĐK:x\ne0\right)\)

\(\Rightarrow x^2-6=x^2+\frac{3}{2}x\)

\(\Rightarrow\frac{3}{2}x=-6\)

\(\Rightarrow x=-4\)

c) \(\frac{3x-2}{4}\ge\frac{3x+3}{6}\)

\(\Rightarrow\frac{3\left(3x-2\right)-2\left(3x+3\right)}{12}\ge0\)

\(\Rightarrow9x-6-6x-6\ge0\)

\(\Rightarrow3x-12\ge0\)

\(\Rightarrow x\ge4\)

d) \(\left(x+1\right)^2< \left(x-1\right)^2\)

\(\Rightarrow x^2+2x+1< x^2-2x+1\)

\(\Rightarrow4x< 0\)

\(\Rightarrow x< 0\)

e) \(\frac{2x-3}{35}+\frac{x\left(x-2\right)}{7}\le\frac{x^2}{7}-\frac{2x-3}{5}\)

\(\Rightarrow\frac{2x-3+5\left(x^2-2x\right)}{35}\le\frac{5x^2-7\left(2x-3\right)}{35}\)

\(\Rightarrow2x-3+5x^2-10x\le5x^2-14x+21\)

\(\Rightarrow6x\le24\)

\(\Rightarrow x\le4\)

f) \(\frac{3x-2}{4}\le\frac{3x+3}{6}\)

\(\Rightarrow\frac{3\left(3x-2\right)-2\left(3x+3\right)}{12}\le0\)

\(\Rightarrow9x-6-6x-6\le0\)

\(\Rightarrow3x\le12\)

\(\Rightarrow x\le4\)

\(a,P=5x\left(2-x\right)-\left(x+1\right)\left(x+9\right)\)

\(=10x-5x^2-\left(x^2+x+9x+9\right)\)

\(=10x-5x^2-x^2-x-9x-9\)

\(=\left(10x-x-9x\right)+\left(-5x^2-x^2\right)-9\)

\(=-6x^2-9\)

Ta thấy: \(x^2\ge0\forall x\)

\(\Rightarrow-6x^2\le0\forall x\)

\(\Rightarrow-6x^2-9\le-9< 0\forall x\)

hay \(P\) luôn nhận giá trị âm với mọi giá trị của biến \(x\).

\(b,Q=3x^2+x\left(x-4y\right)-2x\left(6-2y\right)+12x+1\)

\(=3x^2+x^2-4xy-12x+4xy+12x+1\)

\(=\left(3x^2+x^2\right)+\left(-4xy+4xy\right)+\left(-12x+12x\right)+1\)

\(=4x^2+1\)

Ta thấy: \(x^2\ge0\forall x\)

\(\Rightarrow4x^2\ge0\forall x\)

\(\Rightarrow4x^2+1\ge1>0\forall x\)

hay \(Q\) luôn nhận giá trị dương với mọi giá trị của biến \(x\) và \(y\).

#\(Toru\)

a: \(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}\le\dfrac{x^2}{7}-\dfrac{2x-3}{5}\)

\(\Leftrightarrow2x-3+5x\left(x-2\right)\le5x^2-7\left(2x-3\right)\)

\(\Leftrightarrow2x-3+5x^2-10x< =5x^2-14x+21\)

=>-8x-3<=-14x+21

=>6x<=24

hay x<=4

b: \(\dfrac{6x+1}{18}+\dfrac{x+3}{12}>=\dfrac{5x+3}{6}+\dfrac{12-5x}{9}\)

=>2(6x+1)+3(x+3)>=6(5x+3)+4(12-5x)

=>12x+2+3x+9>=30x+18+48-20x

=>15x+11>=10x+66

=>5x>=55

hay x>=11

Từ giả thiết suy ra (x + 1)² - 4 ≤ (x - 3)²

Û x² + 2x + 1 - 4 ≤ x² - 6x + 9

Û x² + 2x + 1 - 4 - x² + 6x - 9 ≤ 0

Û 8x ≤ 12

Û x ≤ 3/2

Vậy x ≤ 3/2là giá trị cần tìm.

Đáp án cần chọn là: C

a) Rút gọn E Þ đpcm.

b) Điều kiện xác định E là: x ≠    ± 1  

Rút gọn F ta thu được F = 4 Þ đpcm

Giá trị của biểu thức  6 x + 1 18 + x + 3 12  không nhỏ hơn giá trị của biểu thức 5 x + 3 6 + 12 - 5 x 9  nghĩa là  6 x + 1 18 + x + 3 12   ≥   5 x + 3 6 + 12 - 5 x 9

Ta có:

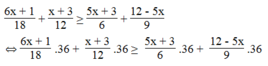
⇔ 12x + 2 + 3x + 9  ≥  30x + 18 + 48 – 20x

⇔ 12x + 3x – 30x + 20x  ≥  18 + 48 – 2 – 9

⇔ 5x  ≥  55

⇔ x  ≥  11

Vậy với x  ≥  11 thì giá trị của biểu thức  6 x + 1 18 + x + 3 12  không nhỏ hơn giá trị của biểu thức 5 x + 3 6 + 12 - 5 x 9