Giải phương trình sau : \(8\cos2x.\sin2x.\cos4x=\sqrt{2}\)

Những câu hỏi liên quan
Giải các phương trình sau: sin 2 x - cos 2 x = cos 4 x
sin 2 x - cos 2 x = cos 4 x ⇔ - cos 2 x = cos 4 x ⇔ 2 cos 3 x . cos x = 0
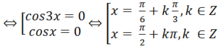
Đúng 0
Bình luận (0)
giải phương trình sau:
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}\)=0
ĐK: \(x\ne\dfrac{\pi}{4}+k\pi;x\ne\dfrac{k\pi}{2}\)
\(\dfrac{2sin^2x+cos4x-cos2x}{\left(sinx-cosx\right)sin2x}=0\)
\(\Leftrightarrow2sin^2x+cos4x-cos2x=0\)
\(\Leftrightarrow2sin^2x-1+cos4x-cos2x+1=0\)
\(\Leftrightarrow2cos^22x-2cos2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\cos2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\2x=k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=k\pi\end{matrix}\right.\)
Đối chiếu điều kiện ta được \(x=-\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
Giải phương trình:
\(3-4\cos2x=\frac{3}{2}.\cos4x+\sqrt{3}\sin2x\left(4-3\cos2x\right)\)
sử dụng công thức biến đổi tích thành tổng hay tổng thành tích để giải các phương trình sau :
a) \(\cos x\cos5x=\cos2x\cos4x\)
b) \(\cos5x\cos4x=\cos3x\cos2x\)
c) \(\sin2x+\sin4x=\sin6x\)
d) \(\sin x+\sin2x=\cos x+\cos2x\)
Giải PT
a1) \(3.\cos4x-2^{ }\cos^23x=1\)
a2) \(2\cos2x-8\cos x+7=\dfrac{1}{\cos x}\)
a3) \(\dfrac{\left(1+\sin x+\cos2x\right)\sin\left(x+\dfrac{\pi}{4}\right)}{1+\tan x}=\dfrac{1}{\sqrt{2}}\cos x\)
a4) \(9\sin x+6\cos x-3\sin2x+\cos2x=8\)
a) Pt \(\Leftrightarrow3.cos4x-\left(cos6x+1\right)=1\)
\(\Leftrightarrow3cos4x-cos6x-2=0\)
Đặt \(t=2x\)
Pttt:\(3cos2t-cos3t-2=0\)
\(\Leftrightarrow3\left(2cos^2t-1\right)-\left(4cos^3t-3cost\right)-2=0\)
\(\Leftrightarrow-4cos^3t+6cos^2t+3cost-5=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cost=1\\cost=\dfrac{1+\sqrt{21}}{4}\left(vn\right)\\cost=\dfrac{1-\sqrt{21}}{4}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}t=k2\pi\\t=\pm arc.cos\left(\dfrac{1-\sqrt{21}}{4}\right)+k2\pi\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\pm\dfrac{1}{2}.arccos\left(\dfrac{1-\sqrt{21}}{4}\right)+k\pi\end{matrix}\right.\) (\(k\in Z\))
Vậy...
a2) \(2cos2x-8cosx+7=\dfrac{1}{cosx}\) (ĐK: \(x\ne\dfrac{\pi}{2}+k\pi\))
\(\Leftrightarrow2.\left(2cos^2x-1\right)-8cosx+7=\dfrac{1}{cosx}\)
\(\Leftrightarrow2.\left(2cos^2x-1\right)cosx-8cos^2x+7cosx=1\)
\(\Leftrightarrow4cos^3x-8cos^2x+5cosx-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\) (tm) (\(k\in Z\))
Vậy...
a3) Đk: \(x\ne-\dfrac{\pi}{4}+k\pi;x\ne\dfrac{\pi}{2}+k\pi\)
Pt \(\Leftrightarrow\dfrac{\left(1+sinx+1-2sin^2x\right).\dfrac{1}{\sqrt{2}}\left(sinx+cosx\right)}{1+\dfrac{sinx}{cosx}}=\dfrac{1}{\sqrt{2}}cosx\)
\(\Leftrightarrow\dfrac{\left(-2sin^2x+sinx+2\right).\left(sinx+cosx\right)cosx}{cosx+sinx}=cosx\)
\(\Leftrightarrow\left(2+sinx-2sin^2x\right).cosx=cosx\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\left(ktm\right)\\2+sinx-2sin^2x=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}cosx=0\left(ktm\right)\\sinx=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{6}+k2\pi\\x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\) (\(k\in Z\))
Vậy...
Đúng 1
Bình luận (2)
a4) Pt \(\Leftrightarrow9sinx+6cosx-6sinx.cosx+1-2sin^2x=8\)
\(\Leftrightarrow6cosx\left(1-sinx\right)-\left(2sin^2x-9sinx+7\right)=0\)
\(\Leftrightarrow6cosx\left(1-sinx\right)-\left(2sinx-7\right)\left(sinx-1\right)=0\)
\(\Leftrightarrow\left(1-sinx\right)\left(6cosx+2sinx+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\6cosx+2sinx=7\left(vn\right)\end{matrix}\right.\) (\(6cosx+2sinx=7\) vô nghiệm do \(6^2+2^2< 7^2\))
\(\Rightarrow sinx=1\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi;k\in Z\)
Vậy...
Đúng 1
Bình luận (0)
Giải các phương trình:
\(a,sin4x.cosx-sin3x=0\)
\(b,sin2x+\sqrt{3}cos2x=\sqrt{2}\)
a, \(sin4x.cosx-sin3x=0\)
\(\Leftrightarrow\dfrac{1}{2}sin5x+\dfrac{1}{2}sin3x-sin3x=0\)
\(\Leftrightarrow sin5x=sin3x\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=3x+k2\pi\\5x=\pi-3x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{8}+\dfrac{k\pi}{4}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
b, \(sin2x+\sqrt{3}cos2x=\sqrt{2}\)
\(\Leftrightarrow\dfrac{1}{2}sin2x+\dfrac{\sqrt{3}}{2}cos2x=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+\dfrac{\pi}{3}=\dfrac{\pi}{4}+k2\pi\\2x+\dfrac{\pi}{3}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{24}+k\pi\\x=\dfrac{5\pi}{24}+k\pi\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải phương trình lượng giác sau:
a) 2sin2x.cos2x+\(\sqrt{3}\)cos4x=\(-\sqrt{2}\)
b) \(sin2x+sin^2x=\frac{1}{2}\)
c) \(cos^2x-\sqrt{3}sin2x=1+sin^2x\)
d) \(5sin2x-6cos^2x=13\)
e) \(2sin3x+sin2x=\sqrt{3}cos2x\)
a.
\(sin4x+\sqrt{3}cos4x=-\sqrt{2}\)
\(\Leftrightarrow\frac{1}{2}sin4x+\frac{\sqrt{3}}{2}cos4x=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(4x+\frac{\pi}{3}\right)=-\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x+\frac{\pi}{3}=-\frac{\pi}{4}+k2\pi\\4x+\frac{\pi}{3}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
b.
\(2sin2x+2sin^2x=1\)
\(\Leftrightarrow2sin2x+1-cos2x=1\)
\(\Leftrightarrow2sin2x=cos2x\)
\(\Leftrightarrow tan2x=\frac{1}{2}\)
\(\Leftrightarrow2x=arctan\left(\frac{1}{2}\right)+k\pi\)
\(\Leftrightarrow...\)
c.
\(cos^2x-sin^2x-\sqrt{3}sin2x=1\)
\(\Leftrightarrow cos2x-\sqrt{3}sin2x=1\)
\(\Leftrightarrow\frac{1}{2}cos2x-\frac{\sqrt{3}}{2}sin2x=\frac{1}{2}\)
\(\Leftrightarrow cos\left(2x+\frac{\pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow...\)
d.
\(5sin2x-3\left(1+cos2x\right)=13\)
\(\Leftrightarrow5sin2x-3cos2x=16\)
Do \(5^2+\left(-3\right)^2< 16^2\) nên pt vô nghiệm
e.
\(\Leftrightarrow sin3x=\frac{\sqrt{3}}{2}cos2x-\frac{1}{2}sin2x\)
\(\Leftrightarrow cos\left(3x-\frac{\pi}{2}\right)=cos\left(2x-\frac{\pi}{6}\right)\)
\(\Leftrightarrow...\)
Giải phương trình: \(cos2x+\sqrt{3}sin2x+\sqrt{3}sinx-cosx=4\).
`cos 2x+\sqrt{3}sin 2x+\sqrt{3}sin x-cos x=4`
`<=>1/2 cos 2x+\sqrt{3}/2 sin 2x+\sqrt{3}/2 sin x-1/2 cos x=2`
`<=>sin(\pi/6 +2x)+sin(x-\pi/6)=2`
Vì `-1 <= sin (\pi/6 +2x) <= 1`
`-1 <= sin (x-\pi/6) <= 1`
Dấu "`=`" xảy ra `<=>{(sin(\pi/6+2x)=1),(sin(x-\pi/6)=1):}`
`<=>{(\pi/6+2x=\pi/2+k2\pi),(x-\pi/6=\pi/2+k2\pi):}`
`<=>{(x=\pi/6+k\pi),(x=[2\pi]/3+k2\pi):}` `(k in ZZ)`
Đúng 1
Bình luận (1)
giải phương trình :(sin2x-4cos2x)(sin2x-2sinxcosx) = 2 cos4x
(sin2x - 4cos2x)(sin2x - 2sinx.cosx) = 2cos4x
⇔ (5sin2x - 4)(sin2x - sin2x) = 2cos4x
⇔ \(\left(\dfrac{5-5cos2x}{2}-4\right)\left(\dfrac{1-cos2x}{2}-sin2x\right)\)= 2cos4x
⇔ \(\dfrac{5-5cos2x-8}{2}.\dfrac{1-cos2x-2sin2x}{2}\) = 2cos4x
⇔ (5cos2x + 3)(cos2x + 2sin2x - 1) = 8cos4x
⇔ 5cos22x + 5cos2x.sin2x + 3cos2x + 6sin2x - 3 = 8cos4x
⇔ 5.\(\dfrac{1+cos4x}{2}\) + \(\dfrac{5}{2}sin4x\) + 3cos2x + 6sin2x - 3 = 8cos4x
⇔ \(\dfrac{5}{2}cos4x+\dfrac{5}{2}sin4x+3cos2x+6sin2x-\dfrac{1}{2}\) = 8cos4x
⇔ 5cos4x + 5sin4x + 6cos2x + 12sin2x - 1 = 16cos4x
VP = 16cos4x = 16 . \(\dfrac{\left(1+cos2x\right)^2}{4}\) = 4. (1 + cos2x)2
VP = 4 . (1 + 2cos2x + cos22x)
VP = 4 + 8cos2x + 4 . \(\dfrac{1+cos4x}{2}\)
VP = 6 + 8cos2x+ 2cos4x
Vậy 3cos4x + 5sin4x - 2cos2x + 12sin2x - 7 = 0
Đúng 1
Bình luận (0)






















