hp tam giác abc có AB=10cm bc=25cm ca=15cm đg fân giác trongvà ngoái góc b cát ac tại m và n tính do dài đường trungtuyến be cua tam giác mbn

Những câu hỏi liên quan
hp tam giác abc có AB=10cm bc=25cm ca=15cm đg fân giác trongvà ngoái góc b cát ac tại m và n tính do dài đường trungtuyến be cua tam giác mbn
help me giup m với mình cần trong 15 phút nx r
- Hơi lâu ấy :)
- Xét tam giác ABC có:
BM là đường phân giác trong (gt)
=>\(\dfrac{BC}{AB}=\dfrac{MC}{AM}\)(định lí đường phân giác).
=>\(\dfrac{BC+AB}{AB}=\dfrac{AC}{AM}\)
=>\(AM=\dfrac{AB.AC}{AB+BC}=\dfrac{10.15}{10+25}=3,75\)(cm)
- Xét tam giác ABC có:
BN là đường phân giác ngoài (gt)
=>\(\dfrac{BC}{AB}=\dfrac{NC}{NA}\)(định lí đường phân giác)
=>\(\dfrac{BC-AB}{AB}=\dfrac{AC}{NA}\)
=>\(NA=\dfrac{AB.AC}{BC-AB}=\dfrac{10.15}{25-15}=15\)(cm)
=>MN=NA+AM=15+3,75=18,75 (cm)
- Ta có: BM, BN lần lượt là đường phân giác trong của góc B (gt)
=> Góc MBN=900 (định lí về góc tạo bởi 2 đường phân giác của 2 góc kề bù).
- Xét tam giác MBN vuông tại B có:
BE là trung tuyến ứng với cạnh huyền MN (gt)
=>BE=MN/2=18,75/2=9,375(cm)
Đúng 2
Bình luận (1)
Cho tam giác ABC vuông tại A có AB=6cm;BC=10cm. Trên canh BC lấy điểm M sao cho BM=18 cm từ điểm M kẻ đường thẳng vuông góc với BC cắt đường thẳng AB AC lần lược là N và P .cm tam giác ABC=tam giác MBN tính độ dài BN ,B/PA.PC=PM.PN
a)
Xét tam giác BAC vuông tại A và tam giác BMN vuông tại M có:
\(\widehat{BAC}\)=\(\widehat{BMN}\)
=> Tam giác BAC ᔕ Tam giác BMN (g-g)
=> BA/BM=BC/BN
=> BN=BM.\(\dfrac{BC}{BA}\)=18.\(\dfrac{20}{12}\)=30cm
b)
Xét tam giác PAN vuông tại A và tam giác PMC vuông tại M có
\(\widehat{APN}\)=\(\widehat{MPC}\) (đối đỉnh)
=> Tam giác PAN ᔕ Tam giác PMC (g-g)
=> \(\dfrac{PA}{PM}\)=\(\dfrac{PN}{PC}\)
=> PA.PC=PM.PN (đpcm)
Đúng 1
Bình luận (0)
Cho tam giác CBM cân tại C có CA là đường cao, CA= 15cm, BC= 25cm.
a) Tính AB và so sánh các góc của tam giác ABC.
b) Gọi H là trung điểm của AC, từ H vẽ đường thẳng vuông góc với AC cắt BC tại E. Chứng minh tam giác EHA = tam giác EHC và tam giác ABE cân tại E.
MN GIẢI GIÚP MIK VỚI Ạ !!
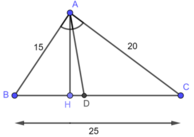
Cho tam giác ABC có AB=15cm, AC=20cm,BC=25cm. Đường phân giác góc BAC cắt BC tại D
a) tính độ dài DB và DC
b) tính tỉ số diện tích tam giác ABC và tam giác ACD
a) Xét tam giác ABC có:
BD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{15}{20}=\dfrac{3}{4}\)(tính chất)
\(\Rightarrow\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{BC}{7}=\dfrac{25}{7}\)(tính chất dãy tỉ số bằng nhau)
\(\Rightarrow\left\{{}\begin{matrix}DB=\dfrac{25.3}{7}=\dfrac{75}{7}\left(cm\right)\\DC=\dfrac{25.4}{7}=\dfrac{100}{7}\left(cm\right)\end{matrix}\right.\)
b) Kẻ đường cao AH của tam giác ABC
\(\Rightarrow\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.AH.DC}{\dfrac{1}{2}.AH.BC}=\dfrac{DC}{BC}=\dfrac{100}{7}:25=\dfrac{4}{7}\)
Đúng 1
Bình luận (0)
a: Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{15}=\dfrac{CD}{20}\)
mà BD+CD=25cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{25}{35}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{75}{7}cm;CD=\dfrac{100}{7}cm\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB=15cm, AC=20cm,BC=25cm. Đường phân giác góc BAC cắt BC tại D
a) tính độ dài DB và DC
b) tính tỉ số diện tích tam giác ABC và tam giác ACD
Hình tự vẽ lấy nhé
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
\(\Rightarrow\frac{DB}{DC}=\frac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
\(\Rightarrow\frac{DB}{DB+DC}=\frac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
\(\Rightarrow\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}\left(cm\right)\)
b) Kẻ \(AH\perp BC\)
Ta có: \(S_{ABD}=\frac{1}{2}AH.BD\)
\(S_{ACD}=\frac{1}{2}AH.CD\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.CD}=\frac{BD}{DC}\)
Mà \(\frac{DB}{DC}=\frac{15}{12}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{3}{4}\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=15cm, AC=20cm,BC=25cm. Đường phân giác góc BAC cắt BC tại D
a) tính độ dài DB và DC
b) tính tỉ số diện tích tam giác ABC và tam giác ACD
c)Cho tam giác ABC có diện tích bằng F tính diện tích tam giác ABD và diện tích tam giác ACD theo F
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)
Đúng 0
Bình luận (0)
Tam giác ABC có AB = 15cm, AC = 20cm, BC = 25cm. Đường phân giác góc BAC cắt cạnh BC tại D. Tính độ dài các đoạn thẳng DB và DC.

Trong △ ABC, ta có: AD là đường phân giác của (BAC)
Suy ra: ![]() (tính chất đường phân giác)
(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên ![]()
Suy ra: ![]() (tính chất tỉ lệ thức)
(tính chất tỉ lệ thức)
Suy ra: 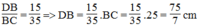
Đúng 0
Bình luận (0)
Tam giác \(ABC\) có \(AB = 15cm,AC = 20cm,BC = 25cm\). Đường phân giác của góc \(BAC\)cắt \(BC\) tại \(D\). Qua \(D\) vẽ \(DE//AB\left( {E \in AC} \right)\).
a) Tính độ dài các đoạn thẳng \(BD,DC\) và \(DE\).
b) Chứng minh \(ABC\) là tam giác vuông. Tính diện tích tam giác \(ABC\).
c) Tính diện tích tam giác \(ADB,ADE\) và \(DCE\).
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
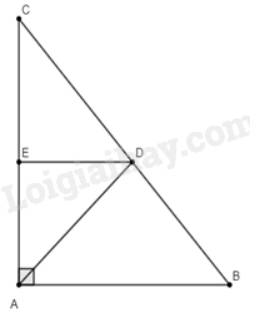
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
Đúng 0
Bình luận (0)
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=25/7
=>DB=75/7cm; DC=100/7cm
Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/15=100/7:25=4/7
=>DE=60/7cm
b: Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
=>S ABC=1/2*15*20=10*15=150cm2
c: DB/DC=3/7
=>S ABD/S ACB=3/7
=>S ABD=150*3/7=450/7cm2
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A, AB=15cm,BC=10cm, đường phân giác của góc B cắt ac tại D
a/ tính AD, DC
b/ Đường vuông góc với BD tại B cắt đường Thẳng AC kéo dài tại E. Chứng minh BE là đường Phân giác ngoài tại đỉnh B của tam giác ACB và ính EC, EA,BD























