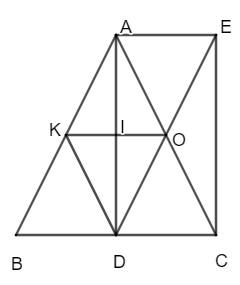
Cho \(\Delta ABC\) cân tại A, đường cao AD, O là trung điểm của AC, điểm E đói cứng với điểm D qua O.
a) Cm: AECD là hình chữ nhật
b) Cm:Gọi I là trung điểm của AD
c) Cho AB = 10cm, BC = 12cm. Tính diện tích tam giác OAD
d) Đường thẳng OI cắt AB tại K. Tìm điều kiện của tam giác ABC để AEDK là hnhf thang cân
Các bạn giúp mình câu d với ạ