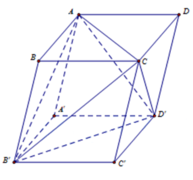
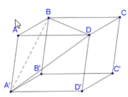
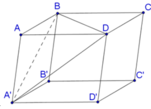
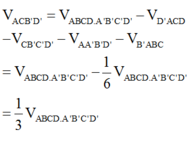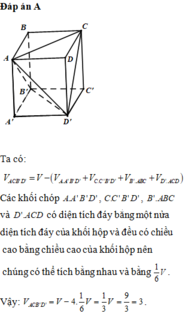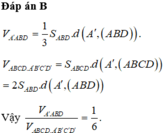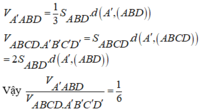Cho hình hộp ABCD.A'B'C'D'. Tính tỉ số thể tích khối hộp đó và thể tích của khối tứ diện ACB'D' ?
Gọi S là diện tích đáy ABCD và h là chiều cao của khối hộp. Chia khối hộp thành khối tứ diện ACB’D’ và bốn khối chóp A.A’B’D’, C.C’B’D’, B’.BAC và D’. DAC. Ta thấy bốn khối chóp sau đều có diện tích đáy bằng và chiều cao bằng h, nên tổng các thể tích của chúng bằng
.
Từ đó suy ra thể tích của khối tứ diện
ACB’D’=. Do đó tỉ số của thể tích khối hộp đó và thể tích của khối tứ diện ACB’D’ bằng 3.
Đúng 0
Bình luận (0)
Cho khối hộp A B C D . A ' B ' C ' D ' . Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB'D'
A. 7 3
B. 3
C. 8 3
D. 2
Khối hộp ABCD.ABCD. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACBD. A.
7
3
B.
3
C.
8
3
D.
2
Đọc tiếp
Khối hộp ABCD.A'B'C'D'. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB'D'.
A. 7 3
B. 3
C. 8 3
D. 2
Cho hình hộp chữ nhật ABCD.ABCD có AB a, BC b, AAc. Gọi E và F lần lượt là những điểm thuộc các cạnh BB và DD sao cho BEdfrac{1}{2}EB; DFdfrac{1}{2}FD. Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.ABCD thành hai khối đa diện (H) và (H). Gọi (H) là khối đa diện chứa đỉnh A. Hãy tính thể tích của (H) và tỉ số thể tích của (H), (H) ?
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, AA'=c. Gọi E và F lần lượt là những điểm thuộc các cạnh BB' và DD' sao cho \(BE=\dfrac{1}{2}EB'\); \(DF=\dfrac{1}{2}FD'\). Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A'B'C'D' thành hai khối đa diện (H) và (H'). Gọi (H') là khối đa diện chứa đỉnh A'. Hãy tính thể tích của (H') và tỉ số thể tích của (H), (H') ?
Cho hình hộp ABCD.A'B'C'D' Tính tỉ số thể tích của khối tứ diện BDA'C' và khối hộp ABCD.A'B'C'D'
A. 1 5
B. 2 3
C. 1 3
D. 2 5
Phương pháp:
Phân chia khối hộp ra các phần, lập tỉ số thể tích.
Cách giải:

Gọi V là thể tích khối hộp ABCD.A'B'C'D'
Ta có: ![]()
= 1 6 V
Mà ![]()
![]()
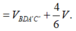
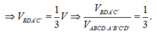
Chọn: C
Đúng 0
Bình luận (0)
Cho khối hộp ABCD.A'B'C'D có thể tích bằng 9. Tính thể tích khối tứ diện ACB'D'.
A. 3
B. 9 2
C. 6
D. 27 4
Cho khối hộp ABCD.A'B'C'D'. Tính tỉ số thể tích của khối tứ diện ABDA' và khối hộp ABCD.A'B'C'D'
A. 1 3
B. 1 6
C. 1 2
D. 6
Cho khối hộp
ABCD
.
A
B
C
D
. Tính tỉ số thể tích của khối tứ diện
ABDA
và khối hộp
ABCD
.
A
B
C
D
.
A. 6. B....
Đọc tiếp
Cho khối hộp ABCD . A ' B ' C ' D ' . Tính tỉ số thể tích của khối tứ diện ABDA ' và khối hộp ABCD . A ' B ' C ' D ' .
A. 6.
B. 1 6
C. 1 3
D. 1 2
Cho khối hộp
A
B
C
D
.
A
B
C
D
. Tính tỉ số thể tích của khối tứ diện
A
B
D
A
và khối hộp
A
B
C
D
.
A
B
C
D
A.
1
3
B.
1
6
C.
1...
Đọc tiếp
Cho khối hộp A B C D . A ' B ' C ' D ' . Tính tỉ số thể tích của khối tứ diện A B D A ' và khối hộp A B C D . A ' B ' C ' D '
A. 1 3
B. 1 6
C. 1 2
D. 6
Cho hình hộp
A
B
C
D
.
A
B
C
D
.
Tính tỉ số thể tích của khối tứ diện
A
C
B
D
và khối hộp đã cho. A. 1/3 B. 1/6 C. 1/2 D. 1/4
Đọc tiếp
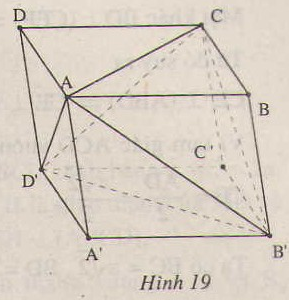
Cho hình hộp A B C D . A ' B ' C ' D ' . Tính tỉ số thể tích của khối tứ diện A ' C ' B D và khối hộp đã cho.
A. 1/3
B. 1/6
C. 1/2
D. 1/4
Đáp án A
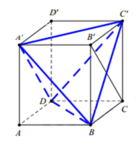
Gọi V là thể tích của khối hộp A B C D . A ' B ' C ' D ' . Khi đó
V A B C D . A ' B ' C ' D ' = V A ' . A B C D + V C . B C D + V D . A ' C ' D ' + V B . A ' B ' C ' + V A . C ' B D
= V 6 + V 6 + V 6 + V 6 + V A . C ' B D = 2 V 3 + V A ' . C ' B D → V A ' . C ' B D = V 3
Vậy tỉ số cần tính là V A ' C ' B D V A B C D . A ' B ' C ' D ' = 1 3 .
Đúng 0
Bình luận (0)