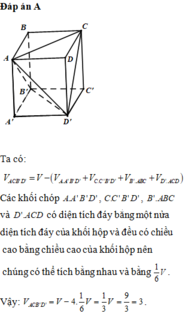Các câu hỏi tương tự
Cho hình hộp ABCD.ABCD có thể tích là V. Tính thể tích của khối tứ diện theo V.
A
.
1
6
V
B
.
2
3
V
C
.
1
3
V
D
.
1
2
V
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có thể tích là V. Tính thể tích của khối tứ diện theo V.
A . 1 6 V
B . 2 3 V
C . 1 3 V
D . 1 2 V
Cho hình hộp ABCD.ABCD có thể tích bằng 12
c
m
3
Tính thể tích của tứ diện ABCD A. 2
c
m
3
c
m
3
B. 3
c...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có thể tích bằng 12 c m 3 Tính thể tích của tứ diện AB'CD'
A. 2 c m 3 c m 3
B. 3 c m 3
C. 4 c m 3
D. 5 c m 3
Cho khối hộp ABCD.ABCD. Mặt phẳng (P) đi qua trung điểm của AB, AD và CC chia khối hộp thành hai đa diện. Khối chứa đỉnh D có thể tích là
V
1
, khối chứa đỉnh B có thể tích là
V
2
Khi đó ta có
A
.
V
1
V
2
1
2...
Đọc tiếp
Cho khối hộp ABCD.A'B'C'D'. Mặt phẳng (P) đi qua trung điểm của AB, A'D' và CC' chia khối hộp thành hai đa diện. Khối chứa đỉnh D có thể tích là V 1 , khối chứa đỉnh B có thể tích là V 2 Khi đó ta có
A . V 1 V 2 = 1 2
B . V 1 V 2 = 3 4
C . V 1 V 2 = 1
D V 1 V 2 = 1 3
Cho khối hộp chữ nhật ABCD.ABCD có thể tích bằng 2018. Biết M, N, P lần lượt nằm trên các cạnh AA, BB, CC sao cho Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng
Đọc tiếp
Cho khối hộp chữ nhật ABCD.A'B'C'D' có thể tích bằng 2018. Biết M, N, P lần lượt nằm trên các cạnh AA', BB', CC' sao cho 
Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Thể tích khối đa diện nhỏ hơn bằng
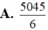
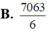
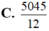
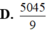
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Khi đó thể tích của khối tứ diện AACD bằng:
A
.
1
2
a
3
B
.
a
3
C
.
1
6
a
3
D
.
1
3
a...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khi đó thể tích của khối tứ diện AA'C'D' bằng:
A . 1 2 a 3
B . a 3
C . 1 6 a 3
D . 1 3 a 3
Cho hình lập phương ABCD.ABCD có cạnh là a. Tính thể tích khối tứ diện ABCD theo a? A.
a
3
6
B.
a
3
2
C.
a
3
4
D. ...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh là a. Tính thể tích khối tứ diện ABC'D' theo a?
A. a 3 6
B. a 3 2
C. a 3 4
D. a 3 3
Cho hình hộp chữ nhật ABCD.ABCD có ABa, AA2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
π
a
3
2
Tính thể tích V của hình hộp chữ nhật ABCD.ABCD.
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AA'=2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π a 3 2 Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
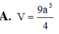
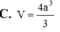
Cho hình lập phương ABCD.ABCD có cạnh bằng a . Gọi O và O lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B C và CD. Tính thể tích khối tứ diện OOMN
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi M và N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN
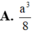
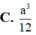
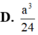
Cho khối tứ diện ABCD có thể tích
V
0
. Dựng hình hộp sao cho AB, AC, AD là ba cạnh của hình hộp. Tính thể tích V của khối hộp đó.
Đọc tiếp
Cho khối tứ diện ABCD có thể tích V 0 . Dựng hình hộp sao cho AB, AC, AD là ba cạnh của hình hộp. Tính thể tích V của khối hộp đó.
