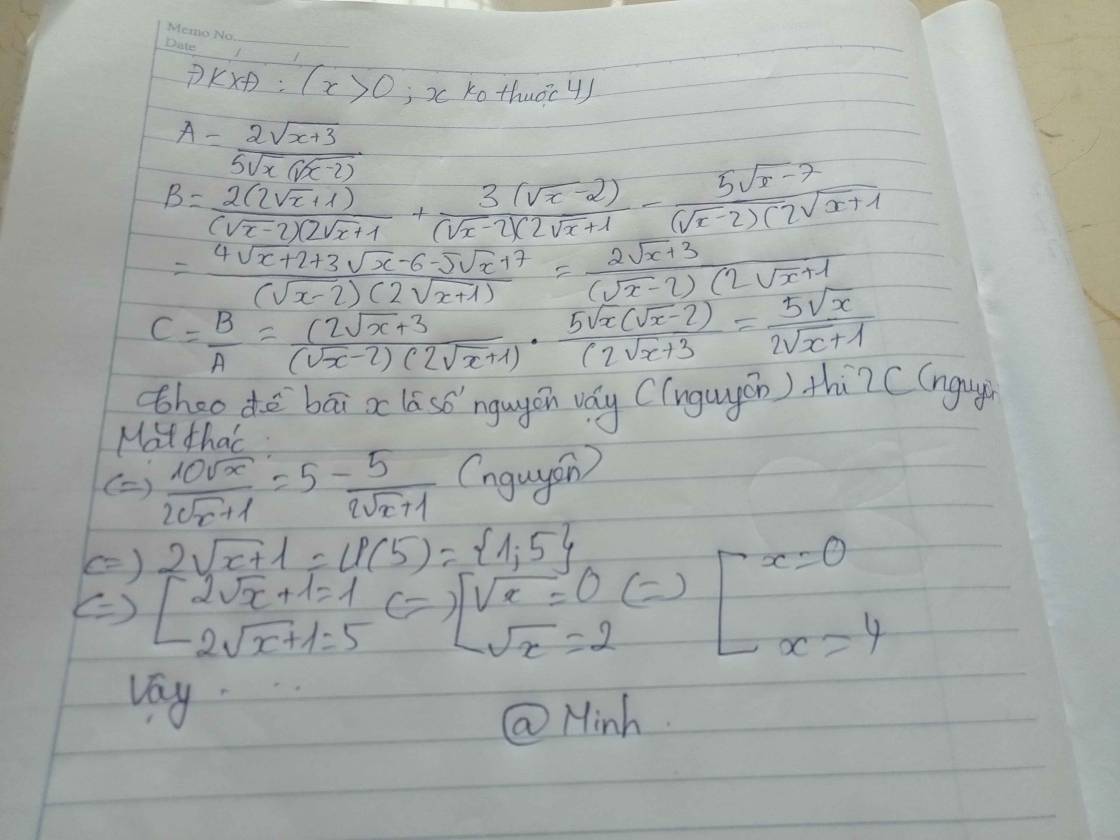em tham khảo

Ta có: 

\(\sqrt{\dfrac{7+3\sqrt{5}}{2}}\)

\(=\sqrt{\dfrac{2\cdot\left(7+3\sqrt{5}\right)}{2\cdot2}}\)

\(=\sqrt{\dfrac{14+6\sqrt{5}}{4}}\)

\(=\sqrt{\dfrac{\left(\sqrt{5}\right)^2+2\cdot\sqrt{5}\cdot3-3^2}{2^2}}\)

\(=\sqrt{\dfrac{\left(\sqrt{5}+3\right)^2}{2^2}}\)

\(=\dfrac{3+\sqrt{5}}{2}\)

Mà: \(\dfrac{3+\sqrt{5}}{2}=a+b\sqrt{5}\)

Nên:  \(\dfrac{3+\sqrt{5}}{2}=\dfrac{3}{2}+\dfrac{\sqrt{5}}{2}=\dfrac{3}{2}+\dfrac{1}{2}\sqrt{5}\)

Vậy: \(a=\dfrac{3}{2};b=\dfrac{1}{2}\)

\(\Rightarrow a+b=\dfrac{3}{2}+\dfrac{1}{2}=\dfrac{4}{2}=2\)

\(\sqrt{\dfrac{7+3\sqrt{5}}{2}}=\sqrt{\dfrac{14+6\sqrt{5}}{4}}=\sqrt{\left(\dfrac{3+\sqrt{5}}{2}\right)^2}\)

\(=\dfrac{3+\sqrt{5}}{2}\)

=>a=3/2; b=1/2

a+b=3/2+1/2=2

a: Khi x=25 thì \(A=\dfrac{7}{5+8}=\dfrac{7}{13}\)

b: \(B=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)+2\sqrt{x}-24}{x-9}\)

\(=\dfrac{x+5\sqrt{x}-24}{x-9}=\dfrac{\left(\sqrt{x}+8\right)\left(\sqrt{x}-3\right)}{x-9}=\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\)

c: P=A*B

\(=\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\cdot\dfrac{7}{\sqrt{x}+8}=\dfrac{7}{\sqrt{x}+3}\)

P là số nguyên

=>căn x+3 thuộc Ư(7)

=>căn x+3=7

=>x=16

a) Ta có: \(\left(7\sqrt{48}+3\sqrt{27}-2\sqrt{12}\right)\cdot\sqrt{3}\)

\(=\left(7\cdot4\sqrt{3}+3\cdot3\sqrt{3}-2\cdot2\sqrt{3}\right)\cdot\sqrt{3}\)

\(=33\sqrt{3}\cdot\sqrt{3}\)

=99

b) Ta có: \(\left(12\sqrt{50}-8\sqrt{200}+7\sqrt{450}\right):\sqrt{10}\)

\(=\left(12\cdot5\sqrt{2}-8\cdot10\sqrt{2}+7\cdot15\sqrt{2}\right):\sqrt{10}\)

\(=\dfrac{85\sqrt{2}}{\sqrt{10}}=\dfrac{85}{\sqrt{5}}=17\sqrt{5}\)

c) Ta có: \(\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\sqrt{8}\right)\cdot3\sqrt{6}\)

\(=\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{4}\cdot2\sqrt{2}\right)\cdot3\sqrt{6}\)

\(=\left(2\sqrt{6}-4\sqrt{3}+3\sqrt{2}\right)\cdot3\sqrt{6}\)

\(=36-36\sqrt{2}+18\sqrt{3}\)

d) Ta có: \(3\sqrt{15\sqrt{50}}+5\sqrt{24\sqrt{8}}-4\sqrt{12\sqrt{32}}\)

\(=3\cdot\sqrt{75\sqrt{2}}+5\cdot\sqrt{48\sqrt{2}}-4\sqrt{48\sqrt{2}}\)

\(=3\cdot5\sqrt{2}\cdot\sqrt{\sqrt{2}}+4\sqrt{3}\sqrt{\sqrt{2}}\)

\(=15\sqrt{\sqrt{8}}+4\sqrt{\sqrt{18}}\)

a,=\(\left(28\sqrt{3}+9\sqrt{3}-4\sqrt{3}\right).\sqrt{3}\)

   \(=28.3+9.3-4.3=99\)

b,\(=\left(60\sqrt{2}-80\sqrt{2}+175\sqrt{2}\right):\sqrt{10}\)

  \(=155\sqrt{2}:\sqrt{10}=\dfrac{155}{\sqrt{5}}\)

d,Ta có:\(3\sqrt{15\sqrt{50}}+5\sqrt{24\sqrt{8}}-4\sqrt{12\sqrt{32}}\)

        \(=3\sqrt{75\sqrt{2}}+5\sqrt{48\sqrt{2}}-4\sqrt{48\sqrt{2}}\)

        \(=15\sqrt{3\sqrt{2}}+20\sqrt{3\sqrt{2}}-16\sqrt{3\sqrt{2}}\)

        \(=19\sqrt{3\sqrt{2}}\)

n tiến tới đâu bạn?

Ok, nó là dạng vô cùng/ vô cùng, sử dụng ngắt vô cùng bé bậc thấp

\(\lim\limits_{n\rightarrow+\infty}\dfrac{\sqrt[3]{an^3+5n^2-7}}{\sqrt{3n^2-n+2}}\) 

Ở tử thấy số mũ là 1; ở mẫu số mũ là 1

\(\Rightarrow\lim\limits_{n\rightarrow+\infty}\dfrac{\sqrt[3]{an^3+5n^2-7}}{\sqrt{3n^2-n+2}}=\lim\limits_{n\rightarrow+\infty}\dfrac{n\sqrt[3]{a}}{n\sqrt{3}}=\dfrac{\sqrt[3]{a}}{\sqrt{3}}\)

\(\Rightarrow\dfrac{\sqrt[3]{a}}{\sqrt{3}}=b\sqrt{3}+c\)

\(\Leftrightarrow\sqrt[3]{a}.\dfrac{\sqrt{3}}{3}+0=b\sqrt{3}+c\Rightarrow\left\{{}\begin{matrix}c=0\\\dfrac{\sqrt[3]{a}}{3}=b\end{matrix}\right.\)

\(\Rightarrow P=\dfrac{a}{b^3}=\dfrac{a}{\dfrac{a}{27}}=27\)

Ta có \(\sqrt{8a^2+56}=\sqrt{8\left(a^2+7\right)}=2\sqrt{2\left(a^2+ab+2bc+2ca\right)}\)

\(=2\sqrt{2\left(a+b\right)\left(a+2c\right)}\le2\left(a+b\right)+\left(a+2c\right)=3a+2b+2c\)

Tương tự \(\sqrt{8b^2+56}\le2a+3b+2c;\)\(\sqrt{4c^2+7}=\sqrt{\left(a+2c\right)\left(b+2c\right)}\le\frac{a+b+4c}{2}\)

Do vậy \(Q\ge\frac{11a+11b+12c}{3a+2b+2c+2a+3b+2c+\frac{a+b+4c}{2}}=2\)

Dấu "=" xảy ra khi và chỉ khi \(\left(a,b,c\right)=\left(1;1;\frac{3}{2}\right)\)

a) \(P=1957\)

b) \(S=19.\)

\(a;b\ge-7\) \(bđt\) \(minicopxki\)

\(\Rightarrow\sqrt{a+7}+\sqrt{b+7}=\sqrt{\sqrt{a}^2+\sqrt{7}^2}+\sqrt{\sqrt{b}^2+\sqrt{7}^2}\ge\sqrt{\left(\sqrt{a}+\sqrt{b}\right)^2+28}\)

\(\Rightarrow9\ge\sqrt{\left(\sqrt{a}+\sqrt{b}\right)^2+28}\)

\(\Leftrightarrow\left(\sqrt{a}+\sqrt{b}\right)^2\le81-28=53\Rightarrow\sqrt{a}+\sqrt{b}\le\sqrt{53}\)

\(dâu"="xảy\) \(ra\Leftrightarrow a=b=13,25\)